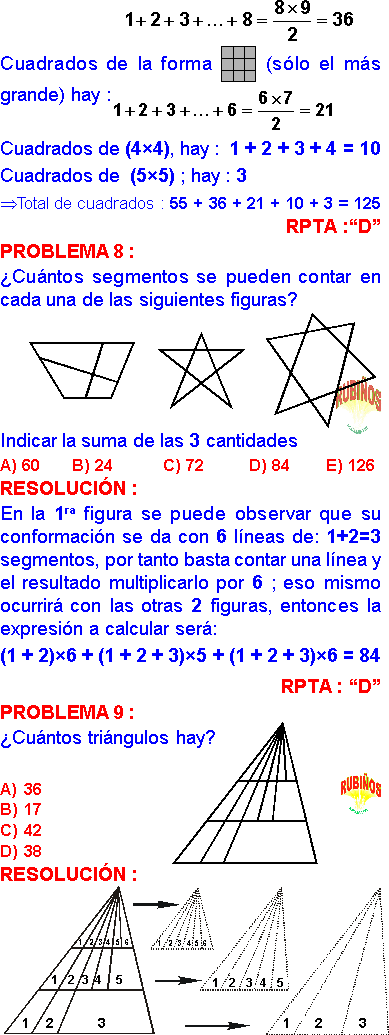
CONTEO DE FIGURAS PROBLEMAS RESUELTOS DE RAZONAMIENTO MATEMÁTICO PREUNIVERSITARIO Y SECUNDARIA PDF
***
CLICK AQUI PARA ver PDF
CLICK AQUI ver VIDEOS
(Método visual) MÉTODOS DE SCHOENK: Consiste en asignar números y/o letras a todas las figuras simples, posteriormente se procede al conteo creciente y ordenado, de figuras de 1 número; al unir 2 números, al unir 3 números, ... etc. ¿Cuántos cuadriláteros hay en?: Resolución: • De 1 número : ninguno • De 2 números : 12 ; 23; 34; 45; 56; 61 • De 3 números : 123 ; 234 ; 345; 456; 563 ; 612 Total de cuadriláteros: 6 6 12 CONTEO MEDIANTE INDUCCIÓN (Fórmula) Consiste en analizar casos particulares a la figura dada (figuras análogas), tratando de encontrar una ley de formación coherente, para luego poder generalizar (encontrar la fórmula). • ¿Cuántos triángulos hay en?: Resolución: Casos Particulares: Para n 1 Para n 2 Para n 3 Figura será Número de triángulos LEY DE FORMACIÓN: 1 (Para 1 espacio) 1 2 (Para 2 espacios) 1 2 3 (Para 3 espacios) para “n” espacios: Número de triángulos: OJO: Este método nos sirve para contar tam¬bién “segmentos”; “cuadriláteros”; “ángulos agu-dos”; “sectores circula¬res”; “hexágonos”; “trapecios”; “letras”; ..... etc. MÉTODO PRÁCTICO: El número de figuras esta dado por: “La mitad de la multiplicación del número de espacios y el consecutivo del número de espacios”. Por ejemplo: 01 ¿Cuántos triángulos hay en?: A) 10 B) 20 C) 15 D) 12 E) 9 Resolución: Método Práctico: Rpta.: C 02 ¿Cuántos segmentos hay en?: A) 36 B) 72 C) 90 D) 45 E) 100 Resolución: “Método Práctico” Rpta.: D 03 ¿Cuántos cuadriláteros hay en?: A) 20 B) 400 C) 140 D) 205 E) 210 Resolución: “Método práctico”: Como hay 20 espacios, luego: Rpta.: E 04 ¿Cuántos ángulos agudos hay?: A) 50 B) 100 C) 2500 D) 800 E) 1275 Resolución: “Por el método práctico” Rpta.: E 05 ¿Cuántos sectores circulares hay en?: A) n B) n2 C) D) E) (n)2 2 Resolución: “Método práctico” Rpta.: D 06 ¿Cuántos hexágonos hay en?: A) 6 B) 16 C) 15 D) 21 E) 42 Resolución: • Contando encontramos 6 espacios, luego: Rpta.: D 07 ¿Cuántos triángulos hay en?: A) 42 B) 36 C) 6 D) 12 E) 21 Resolución: Analizando casos particulares nos daremos cuenta que cumple con el “Método práctico” Rpta.: E 08 ¿Cuántos cuadriláteros hay en?: A) 6 B) 12 C) 16 D) 18 E) 24 Resolución: Contando directamente, encontraremos 18, pero el método más rápido sería: Número de cuadriláteros Rpta.: D En general: 09 ¿Cuántos cuadriláteros hay en?: A) 120 B) 150 C) 250 D) 320 E) 20 Resolución: “Por el método práctico” Rpta.: B 10 ¿Cuántos paralelepípedos hay en?: A) 20 B) 60 C) 125 D) 900 E) 2750 Resolución: Por el método práctico: Rpta.: D MÉTODO PARA CONTAR CUADRADOS Y CUBOS PROBLEMA 01 ¿Cuántos cuadrados hay en?: Resolución: Casos Número Ley de particulares de cuadrados formación n 1 1 12 n 2 1 4 12 22 n 3 1 4 9 12 22 32 Para “n” 12 22 32 n2 PROBLEMA 02 ¿Cuántos cubos hay en?: Resolución: Al igual que lo anterior los cubos se relacionan con la suma de cubos: 13 23 33 n3 PROBLEMA 03 ¿Cuántos cuadrados hay en?: A) 140 B) 120 C) 230 D) 49 E) 343 Resolución: 12 22 32 72 Rpta.: A PROBLEMA 04 ¿Cuántos cubos hay en? A) 64 B) 216 C) 100 D) 220 E) 512 Resolución: Como el cubo es de 4 4 4 13 23 33 43 100 Rpta.: C OJO: El número de cuadrados también se puede calcular así: “Se multiplica los extremos y se suman los resultados” Número de cuadrados 1 4 9 16 30 “Este método nos sirve para contar cuadrados, en una figura no cuadrada”. PROBLEMA 05 ¿Cuántos cuadrados hay en?: A) 20 B) 40 C) 30 D) 42 E) 60 Resolución: Por el método práctico: Número de cuadrados 2 6 12 20 40 Rpta.: B PROBLEMA 06 En el problema “5”, hallar el total de cuadriláteros que no son cuadrados A) 40 B) 60 C) 110 D) 20 E) 5 Resolución: 110 Rpta.: C PROBLEMA 07 ¿Cuántos cubos hay en?: A) 125 B) 60 C) 70 D) 180 E) 720 Resolución: “Aplicando el método de los cuadrados en una figura no cuadrada”. 5 4 3 4 3 2 3 2 1 90 Rpta.: C En General: Conteo de cuadrados: PROBLEMAS DIVERSOS PROBLEMA 01 ¿Cuántos triángulos hay en?: A) 20 B) 30 C) 35 D) 32 E) 36 Resolución: Triángulos: • 1 región: 1 ; 2 ; 3; 4; 5; a; b; c; d; e • 2 regiones: 1a ; 2a; 2b; b3; 3c; c4; 4d; d5; 5e; e1 • 3 regiones: 1a2 ; a6d ; a6c ; 2b3 ; b6d ; b6e; 3c4; c6e; 4d5; 5e1 • 4 regiones: Ninguno • 5 regiones: Hay 5 (simple inspección) 10 10 10 5 35 Rpta.: C PROBLEMA 02 ¿Cuántos triángulos hay en: A) 30 B) 40 C) 20 D) 50 E) 18 Resolución: 3 10 30 Rpta.: A PROBLEMA 03 ¿Cuántos triángulos tienen por lo menos un asterisco en su interior. A) 9 B) 8 C) 10 D) 7 E) 12 Resolución: Rpta.: B PROBLEMA 04 ¿Cuántos cuadrados hay en?: A) 100 B) 93 C) 81 D) 125 E) 64 Resolución: Contando por simple inspección: • Cuadrados de la forma , hay: • Cuadrados de la forma (solo el más grande), hay: • Cuadrados de la forma (sólo el más grande) hay: • Cuadrados de (4 4), hay: 1 2 3 4 10. • Cuadrados de (5 5); hay: 3 • Finalmente. Total de cuadrados: 55 36 21 10 3 125 Rpta.: D PROBLEMA 05 ¿Cuántos triángulos hay en?: A) 3n (n 1) B) 3 (n 1) C) n (n 2) D) E) Resolución: Si la figura fuera así: Habría: triángulos, pero a ésta cantidad, hay que aumentar el número de triángulos de la parte sombreada. Luego el total de triángulos será: n (n 1) n n (n 2) Rpta.: C En general: (Método Práctico) : Donde: m y n indican la cantidad de espacios. PROBLEMA 06 ¿Cuántos triángulos hay en?: A) 30 B) 90 C) 75 D) 165 E) 225 Resolución: Aplicando el método práctico: PROBLEMA 07 ¿Cuántos triángulos hay en total en la siguiente figura? A) 1240 B) 3240 C) 3080 D) 4000 E) 8000 Resolución: Por inducción matemática: 2 1 2 2 6 1 2 2 3 Se está formando la suma de los primeros productos binarios, luego en la figura dada, el número de triángulos será: 1 2 2 3 3 4 20 21 3080 Rpta.: C En general: PROBLEMA 08 En una hoja cuadrada y cuadriculada con “n” cuadraditos por lado, se traza una de las diagonales. ¿Cuántos triángulos se forman como consecuencia de este trazado? A) n B) n (n 1) C) n (n 1) D) E) Resolución: Por inducción matemática: 2 1 2 6 2 3 12 3 4 Rpta.: C PROBLEMA 09 ¿Cuántos triángulos hay en?: A) 62 B) 63 C) 60 D) 71 E) 36 Resolución: Considerando el problema anterior, el número de triángulos será: 3 4 4 5 5 6 1 63 Rpta.: B PROBLEMA 10 ¿Cuántos cuadrados hay en total en? A) 3n 9 B) 9n 6 C) 4n 9 D) 8n 3 E) 8n 9 Resolución: Si todos los cuadrados más grandes fueran así: Habría en total “8n” cuadrados pero la primera le falta “2” cuadrados y al enésimo “7”, entonces realmente hay: 8n 2 7 8n 9 cuadrados Rpta.: E PROBLEMA 11 Hallar el número total de diagonales que se pueden trazar en total en los cuadriláteros mostrados. A) 126 B) 216 C) 252 D) 421 E) 512 Resolución: Como en cada cuadrilátero solo se puede trazar 2 diagonales, luego para calcular el total de diagonales, será suficiente hallar el total de cuadriláteros y multiplicar por 2 esta cantidad; entonces: Rpta.: C PROBLEMA 12 ¿Cuántas pirámides de base cuadrangular hay en el sólido mostrado? A) 98 B) 108 C) 252 D) 72 E) 64 Resolución: Si la figura fuera así: Habría: El cual indica, la cantidad de pirámides ya que cada cuadrilátero es la base de 1 pirámide, pero solo estamos conside¬rando 1 capa vertical, luego en el pro¬blema se observa 7 de éstas capas, enton¬ces : : 36 • 7 252 Rpta.: C PROBLEMA 13 Calcular el número de cuadriláteros en: A) 316 B) 320 C) 310 D) 315 E) 318 Resolución: Si contamos por separado en cada uno de los rectángulos más grandes, se tendrá que: : : : : 168 210 60 318 COMENTARIO : Se resta la intersección ya que al contar por separado se contabiliza 2 veces la intersec-ción y sólo se debe contar una. Rpta.: E PROBLEMA 14 Determinar la cantidad total de triángulos que se pueden contar en la siguiente figura: A) 64 B) 124 C) 208 D) 308 E) 318 Resolución: Por inducción: • Luego para el problema: # de triángulos: 32(10) 12 308 Rpta.: D PROBLEMA 15 ¿Cuántos segmentos hay en la figura? A) 308 B) 632 C) 606 D) 4050 E) 720 Resolución: La figura con la misma cantidad de segmentos será: Por cada línea horizontal hay: segmentos y como existe 21 de éstas líneas, luego habrá: 21 6 126 segmentos horizontales : : 506 126 632 Rpta.: B PROBLEMA 16 ¿Cuántos triángulos hay en?: A) 4n 3 B) 4n 1 C) 4 (n 3) D) 4n 5 E) 2n 1 Resolución: Considerando: • Luego en “n” de estos vértices habrán “4n” triángulos, sin considerar el más grande, pero debemos considerarlo, luego: Total de triángulos: 4n 1 Rpta.: B PROBLEMA 17 ¿Cuántos semicírculos hay en total? A) 12 B) 18 C) 23 D) 32 E) 42 Resolución: Por cada diámetro hay 4 circunferencias, es decir: 2 4 semicircunferencias; pero se observa 4 diámetros, entonces: : 2 4 4 32 Rpta.: D Método Práctico: Nº semicirc. 2 (Nº circunf) (Nº diámetros) Recuerde: Fila 1 1 1 20 211 Fila 2 1 1 2 21 221 Fila 3 1 2 1 4 22 231 Fila 4 1 3 3 1 8 23 241 1 4 6 4 1 16 24 251 ......................... ......................... 1 ...... n ...... n ..... 1 2n 1 Ley de formación: • Los número de los extremos siempre son 1. • Cada número del interior es igual a la suma de sus 2 inmediatos superiores. PROBLEMA 18 ¿De cuántas formas se puede leer la palabra “RAZONA” en la siguiente distribución? A) 64 B) 32 C) 16 D) 36 E) 25 Resolución: Aplicando un método análogo a la formación del triángulo de Pascal: Luego para leer la palabra “RAZONA” se debe recorrer: 32 caminos o formas Rpta.: B Método Práctico: : 2n 1 PROBLEMA 19 ¿De cuántas maneras se puede ir de A a B por el camino más corto? A) 8 B) 16 C) 36 D) 70 E) 62 Resolución: Por el triángulo de Pascal. Número de manera: 70 Rpta.: D EN GENERAL: : PROBLEMA 20 ¿De cuantas formas se puede ir de A a B por el camino más corto? A) 150 B) 180 C) 168 D) 192 E) 149 Resolución: Por el triángulo de Pascal: 180 formas Rpta.: B PROBLEMA 21 ¿De cuántas formas se puede leer la palabra “AMAR”? A) 15 B) 16 C) 20 D) 32 E) 64 Resolución: Por el “Triángulo de Pascal” en ambos lados de la diagonal Total 16 formas Rpta.: B TRAZOS Y FIGURAS (Figuras de un solo Trazo) VÉRTICE PAR (P) Punto donde se en-cuentran o concu-rren un número par de líneas. VÉRTICE IMPAR (I) Punto donde concurren un número impar de líneas: OJO: El objetivo de este acápite es verificar si una figura se puede dibujar de un solo trazo, sin levantar el lápiz del papel ni pasar 2 veces por una misma línea; y para ello debemos tener en cuenta lo si¬guiente: A. PRIMERA REGLA: Si una figura posee sólo puntos pares, se podrá dibujar de un solo trazo y se puede comenzar por cualquier punto y termi-nando en el mismo. Ejemplo: “La figura se puede dibujar de un solo trazo, porque todos sus vértices o puntos de intersección son pares”. B. SEGUNDA REGLA: Si una figura presenta 2 puntos impares, se podrá dibujar de un sólo trazo, siempre y cuando se empiece en uno de los puntos impares y se termine en el otro. Ejemplo: “La figura se puede dibujar de un solo trazo, porque solo presenta 2 puntos impares”. C. TERCERA REGLA: Si la figura presenta más de 2 puntos impares, es imposible dibujarla de un sólo trazo. Ejemplo: Estas figuras nunca se podrá dibujar de un sólo trazo porque poseen más de 2 puntos impares. D. CUARTA REGLA: Si una figura presenta “I” puntos impares (I 2), para dibujarla se repetirá como mínimo: líneas PROBLEMA 22 ¿Cuántas líneas debemos recorrer como mínimo para dibujar la siguiente figura, sin levantar el lapicero? A) 4 B) 6 C) 7 D) 8 E) 9 Resolución: Como tiene 4 vértices impares, entonces tendré que repetir: línea, y como la figura tiene 6 líneas, luego se tendrá que recorrer 7 líneas. Rpta.: C PROBLEMA 23 Como mínimo una araña emplea 15 minutos en recorrer todas las aristas de un cubo construido con un alambre. ¿Qué tiempo empleó en recorrer una arista? A) 1,5 min B) 1 min C) 2 min D) 0,5 min E) 1,25 min Resolución: Como el cubo tiene 8 vértices impares, luego se tendrá que repetir como mínimo: aristas y como el cubo tiene 12 aristas. Entonces para recorrer todo el cubo, se tendrá que recorrer 12 3 15 aristas, pero el enunciado indica: 15 aristas 15 min 1 arista 1 min Rpta.: B PROBLEMA 24 ¿Cuál (es) de los siguientes gráficos se puede realizar de un solo trazo y sin levantar el lápiz? (I) (II) (III) A) sólo II B) I y II C) II y III D) I y III E) todos Resolución: (I) No, porque posee más de 2 vértices impares. (II) Sí, porque posee 2 vértices impares. (III) Sí, porque posee 2 vértices impares. Rpta.: C PROBLEMA 25 Para que la siguiente figura se puede efectuar de un sólo trazo y sin pasar dos veces por el mismo trazo, se debe empezar por: A) A o B B) C o D C) E o F D) G ó H E) Cualquier punto Resolución: Se debe empezar ya sea por “C” o por “D”, por ser puntos impares. Rpta.: B PROBLEMA 26 Una persona debe recorrer todas y cada una de las avenidas interiores en una sola dirección sin recorrer dos veces por una misma avenida, ¿por cuál de las 3 puertas debe salir al finalizar? A) C B) B C) A D) Cualquiera de las tres E) F.D. Resolución: Haciendo el trayecto que debe seguir: Necesariamente debe terminar en un punto impar, es decir en “A”. Rpta.: C PROBLEMA 27 ¿Cuántos cubitos más hay que adicionar como mínimo para formar un cubo sólido completo? A) 26 B) 42 C) 36 D) 34 E) 28 Resolución: Por simple inspección se puede contar 30 cubitos y faltará: 43 30 34 cubitos Rpta.: D PROBLEMA 28 ¿Cuántos cuadrados hay en la figura adjunta? A) 60 B) 68 C) 72 D) 74 E) 70 Resolución: (12 22 32 42) (12 22 32 42 4 3) 72 Rpta.: C PROBLEMA 29 ¿Cuántos triángulos hay en? : A) 420 B) 343 C) 512 D) 421 E) 481 Resolución: Aplicando el método práctico del problema 6, luego: : Rpta.: A PROBLEMA 30 El siguiente gráfico representa una telaraña. ¿Cuántos tramos unió la araña para hacer su tela? A) 40 B) 60 C) 80 D) 120 E) 160 Resolución: Contamos los tramos (segmentos simples), por partes: TOTAL DE TRAMOS 16 4(16) 80 Rpta.: C PROBLEMA 31 ¿Cuántos cuadriláteros que por lo menos tengan 1 asterisco hay en la figura. A) 119 B) 118 C) 120 D) 121 E) 122 Resolución: Por el método del complemento: Rpta.: D PROBLEMA 24 Si la figura está formada por cuadraditos iguales, ¿cuántos cuadrados se contaran en total? A) 56 B) 68 C) 72 D) 84 E) 91 Resolución: # de cuadrados de 1 1: 1 3 5 …… 62 # de cuadrados de 2 2: 2 4 6 8 20 # de cuadrados de 3 3: # de cuadrados de 4 4: 2 # de cuadrados de 5 5 1 Total: 36 20 9 2 1 68 Rpta.: B PROBLEMA 33 ¿Cuántos triángulos hay? A) 2840 B) 930 C) 9455 D) 7281 E) 9331 Resolución: Por inducción: Rpta.: C PROBLEMA 34 Con 28 cerillas se ha construido una rejilla, tal como se muestra en la figura. Si cada cerilla mide 5cm. ¿Cuál es la menor longitud que debe recorrer una hormiga por todas las cerillas? A) 130 cm. B) 120 cm. C) 150 cm. D) 145 cm. E) 160 cm. Resolución: Al haber 4 vértices impares, se repetirá (una cerilla) como mínimo, luego se recorrerá en total: 28 1 29 cerillas, es decir: 29 5 cm. 145 cm. Rpta.: D PROBLEMA 35 ¿Cuántos cuadriláteros contienen un solo asterisco? A) 4 B) 5 C) 6 D) 7 E) 8 Resolución: Por simple inspección: (al ojo) Lo pedido será: 3 3 6 Rpta.: C PROBLEMA 36 Hallar el número de triángulos en: A) 20 B) 25 C) 22 D) 18 E) 21 Resolución: Si todos tuvieran la forma de: Habría: 6 4 24 triángulos; Pero al último le faltan dos triángulos, por lo que sólo hay: 24 2 22 triángulos Rpta.: C PROBLEMA 37 Hallar el número de puntos de intersec¬ción de 102 circunferencias dispuestas tal como se muestra en la figura. A) 640 B) 620 C) 600 D) 612 E) 642 Resolución: Por cada circunferencia menor hay 6 puntos de intersección: • Luego en las 102 circunferencias habrá: 102 6 612 puntos de intersección. Rpta.: D PROBLEMA 38 Hallar el número total de cuadriláteros en la figura adjunta: A) 1740 B) 1830 C) 1810 D) 1780 E) 1870 Resolución: Hay dos tipos de cuadriláteros: Forma Cantidad: 3(30) Luego el total de cuadriláteros será: 58 30 3 30 61 30 1830 Rpta.: B PROBLEMA 39 La figura mostrada es una cuadrícula de 7cm. por 4cm. ¿Cuántos hexágonos de 4cm2 de área hay en la figura? A) 96 B) 108 C) 120 D) 98 E) 112 Resolución: Por cada rectángulo de 2 3 hay 4 hexágonos de 4 cm2 de área tal como se muestra: • Los hexágonos son: 1234, 1654, 6123, 6543 • Por simple inspección contamos los rectángulos de 2 3 y de 3 2, los cuales son en total 27. • Finalmente: : 27 4 108 Rpta.: B PROBLEMA 40 El siguiente sólido está formado por cubitos todos iguales, si pintamos el sólido, ¿cuántos cubitos no tendrán ninguna cara pintada? A) 6 B) 2 C) 4 D) 8 E) 5 Resolución: Como el sólido es de 4 4 3; al pintarlo, los cubitos que no van a tener ninguna cara pintada, serán todos menos los cubitos externos, es decir. Al no considerar a estos últimos 3 quedarán: 2 2 1 4 cubitos Rpta.: C PROBLEMA 41 Calcular el número total de triángulos. A) 1 520 B) 1 540 C) 1 270 D) 1 840 E) 2 100 Resolución: Empezamos contando por la parte superior de horizontal en horizontal, tendremos que: : Rpta.: B PROBLEMA 42 ¿Cuántas semicircunferencias hay en la figura?. A) 10 B) 20 C) 4 D) 8 E) 12 Resolución: Por simple inspección hay: 4 4(4) 20 Rpta.: B PROBLEMA 43 De las figuras ¿cuáles se pueden trazar sin levantar el lápiz y sin repasar las líneas? (IV) (V) A) I ; V B) I ; II ; III C) II ; IV D) II ; V E) II ; III ; IV Resolución: Más de 2 impares (NO) …… Sólo 2 impares (SI) ……… Más de 2 impares (NO) … Todos pares (SI) ………… Más de 2 impares (NO) …… Rpta.: C PROBLEMA 44 Indique el número de triángulos que hay en la siguiente figura: A) 18 B) 14 C) 16 D) 7 E) 8 Resolución: De 1 sólo número : 7 De 2 números : (47); (67); (56); (45) 4 De 3 números : (367); (147) 2 De 7 números : (1234567) 1 Total : 14 Rpta.: B PROBLEMA 45 En la figura consideremos lado a todo segmento que une dos puntos. Es posible trazar una línea curva a partir del punto “A” que interseca a todos los lados de una sola vez y en forma continua regrese al punto “A”. A) Si es posible B) Sólo si se interseca dos veces a un lado. C) Sólo se interseca 3 veces a un lado. D) Sólo si interseca 4 veces a un lado. E) No es posible. Resolución: • Será posible si se interseca 2 veces a un lado, por que la figura que hemos dibu-jado adicionalmente presenta únicamente puntos pares. Rpta.: B PROBLEMA 46 Hallar el máximo número de hexágonos en la siguiente figura. A) 15 B) 18 C) 20 D) 21 E) 22 Resolución: Por simple inspección se cuentan 21 hexágonos (hay de dos formas: y ) Rpta.: D PROBLEMA 47 ¿Cuántos cubitos están en contacto con el cubo número 10? A) 6 B) 12 C) 20 D) 8 E) 14 Resolución: Cualquier cubo que este cubierto todo su alrededor de cubos, estará en contacto con: 6 12 8 26 • El cubo número 10 estará en contacto con todos menos 6, es decir con: 26 6 = 20 Rpta.: C PROBLEMA 48 ¿Cuántos triángulos rectángulos hay como máximo en la siguiente figura? A) 210 B) 320 C) 444 D) 401 E) 4414 Resolución: Por inducción: • Piden: 201 2 1 401 Rpta.: D PROBLEMA 49 Cuántas pirámide de base cuadrada hay en el sólido mostrado. A) 42 B) 49 C) 94 D) 98 E) 96 Resolución: Por cada cuadrado de la base hay 7 pirámides, luego: # de pirámides 7 01 ¿Cuántos segmentos hay? A) 36 B) 44 C) 48 D) 42 E) N.A. 02 ¿Cuántos triángulos hay? A) 48 B) 52 C) 56 D) 50 E) 54 03 ¿Cuántos triángulos hay? A) 118 B) 112 C) 128 D) 113 E) N.A. 04 Dar el número de triángulos A) 29 B) 33 C) 30 D) 31 E) 32 05 ¿Cuántos triángulos hay? A) 30 B) 20 C) 21 D) 22 E) 23 06 ¿Cuántos triángulos hay? A) 21 B) 42 C) 18 D) 24 E) 22 07 ¿Cuántos triángulos hay? A) 102 B) 120 C) 130 D) 100 E) 125 08 ¿Cuántos triángulos hay? A) 70 B) 68 C) 72 D) 28 E) N.A. 09 ¿Cuántos cuadriláteros convexos hay? A) 225 B) 150 C) 165 D) 155 E) 175 10 ¿Cuántos cuadriláteros hay? A) 8 B) 9 C) 6 D) 10 E) N.A. 11 ¿Cuántos cuadriláteros hay? A) 49 B) 62 C) 58 D) 60 E) 59 12 ¿Cuántos cuadriláteros hay? A) 362 B) 358 C) 360 D) 315 E) N.A. 13 Hallar el número de cuadriláteros. A) 7 B) 8 C) 9 D) 10 E) 11 14 ¿Cuántos cuadriláteros hay? A) 234 B) 236 C) 216 D) 252 E) 200 15 ¿Cuántos cuadrados hay? A) 32 B) 29 C) 28 D) 30 E) 31 16 ¿Cuántos cuadriláteros hay? A) 190 B) 194 C) 192 D) 210 E) N.A. 17 ¿Cuántos rectángulos no cuadrados hay en un tablero de Ajedrez? A) 1296 B) 1500 C) 204 D) 1092 E) 1094 18 ¿Cuántas diagonales como máximo se pueden trazar en? A) 246 B) 492 C) 294 D) 282 E) 552 19 Un paralelepípedo de madera es pintado totalmente, luego se corta en cubitos pequeños como muestra la figura. Si se retiran los cubitos con sólo dos caras pintadas. ¿Cuántos cubitos quedarán? A) 48 B) 60 C) 52 D) 64 E) 80 20 ¿Cuántos cuadriláteros no cuadrados hay en la siguiente figura? A) 150 B) 166 C) 156 D) 160 E) 182 21 Hallar el número total de cuadriláteros A) 343 B) 312 C) 323 D) 400 E) 512 22 ¿Cuántos puntos de corte hay en F10? A) 92 B) 184 C) 90 D) 212 E) 421 23 ¿Cuántos cuadriláteros que por lo menos tengan un asterisco hay en la figura? A) 320 B) 132 C) 121 D) 152 E) 201 24 ¿Cuántos puntos de corte hay? A) 100 B) 1000 C) 990 D) 1100 E) 991 25 ¿Cuántos puntos de contacto hay en la siguiente figura? A) 670 B) 572 C) 575 D) 578 E) 570 26 ¿Cuántos triángulos hay en la figura adjunta?