HABILIDAD LÓGICO MATEMÁTICA RESUELTA
PREGUNTA 16 :
Un fabricante obsequia 2 polos por cada 10 polos que compra un cliente. ¿Cuál es la máxima cantidad de polos que recibe como obsequio un cliente que lleve en total 200 polos (entre comprados y obsequiados)?
A) 34
B) 26
C) 30
D) 32
E) 28
PREGUNTA 17 :
Se dispone de tres recipientes no trasparentes y sin graduar. El primero tiene 11 litros de capacidad y está lleno de vino; el segundo y tercer recipientes están vacíos y tienen 3 y 5 litros de capacidad, respectivamente. Si solo se pueden realizar trasvases de un recipiente a otro sin desperdiciar vino en ningún momento, ¿cuántos trasvases como mínimo serán necesarios para que en el primer recipiente queden 10 litros de vino?
A) 4
B) 5
C) 3
D) 6
E) 2
PREGUNTA 18 :
Don Francisco es un albañil dedicado al enchapado de losetas. Dispone de una loseta de forma rectangular de 80 cm de largo por 60 cm de ancho y de un cortador de loseta que corta hasta 60 cm y como máximo tres capas. Si de esta loseta rectangular requiere obtener doce losetas cuadradas, cuyos lados midan 20 cm, como se muestra en la figura, ¿cuántos cortes rectos debe realizar como mínimo para cumplir con lo requerido?
A) 3
B) 5
C) 6
D) 4
E) 2
PREGUNTA 19 :
Para el ingreso al laboratorio de una empresa, su Departamento de Seguridad ha asignado a cada investigador el siguiente diagrama de flujo para determinar un número de salida, el cual debe emplear para ingresar por la puerta de seguridad:
Cada semana, se le asigna a cada investigador un número de ingreso x. Para entrar al laboratorio, se debe digitar en la puerta de seguridad el número de salida obtenido mediante el diagrama de flujo. Si Wilson es un investigador al que esta semana se le asignó el número 107, ¿cuál es el número que debe digitar en la puerta de seguridad?
A) 20
B) 13
C) 19
D) 24
E) 18
PREGUNTA 20 :
La hija de Maribel está casada con Raúl y este, a su vez, es abuelo de Joel. Nancy es madre de Daniela y, a la vez, es abuela de Joel. Si Carlos está casado con Maribel y Nancy es su única hija, ¿cuál es el parentesco familiar de Daniela con Carlos?
A) bisnieta
B) hija
C) nieta
D) sobrina
E) nuera
PREGUNTA 21 :
En una competencia olímpica, participaron cuatro atletas. Al final de la competencia, en la que no hubo empates, se les pregunta sobre los puestos en que llegaron y cada uno de ellos declaró lo siguiente:
• Alberto: “Daniel llegó primero; Bernardo, último”.
• Claudio: “Yo gané la carrera. Alberto llegó segundo”.
• Bernardo: “Yo llegué tercero; Alberto, cuarto”.
• Daniel: “Bernardo llegó segundo; Claudio, cuarto”.
Si cada uno dijo una mentira y una verdad, pero no necesariamente en ese orden, ¿quién llegó tercero y quién, cuarto en ese orden?
A) Daniel - Claudio
B) Bernardo - Claudio
C) Bernardo - Daniel
D) Alberto - Bernardo
E) Claudio - Daniel
PREGUNTA 22 :
Las figuras I, II y III representan tres láminas cuadradas congruentes y transparentes, divididas en cuatro partes congruentes. Si la figura I rota 90° en el sentido horario con respecto a su centro; la figura II, rota 90° en el sentido antihorario con respecto a su centro; y la figura III, rota 360° en sentido horario con respecto a su centro y luego se trasladan dos de ellas, sin rotar, sobre la tercera, ¿qué figura resulta?
PREGUNTA 23 :
Álvaro, Beto, Carlos, Daniel y Fernando, cuyas edades son 21 ; 22 ; 23 ; 24 y 25 años, respectivamente, se encuentran sentados en cinco sillas juntas ubicadas en una misma fila y conversan:
☛ Daniel dice: “hay más de una persona sentada a mi izquierda”.
☛ Beto le dice al que está sentado junto a él, a su izquierda: “tú eres el único que no tiene a nadie sentado a tu izquierda”.
☛ Carlos, que está sentado entre Beto y Daniel, dice: “Fernando está enemistado con Daniel y por eso no se sientan juntos”.
☛ Daniel no está sentado a la derecha de todos.
Las edades de las personas que están sentadas junto a Carlos suman ____ años.
A) 47
B) 45
C) 49
D) 46
E) 43
PREGUNTA 24 :
Cuatro padres de familia, de nombres Abel, César, Fernando y Marcos, tienen una hija cada uno, cuyos nombres son Ana, Camila, Fiona y Micaela, no necesariamente en este orden, las cuales están inscritas en un taller virtual.
Se sabe lo siguiente:
☛ La primera letra de los nombres de los padres no coinciden con la primera letra de los nombres de sus respectivas hijas.
☛ Fiona llama a la casa de Abel y Marcos para preguntar por qué sus hijas no han ingresado al taller virtual el día de hoy.
☛ Las mejores amigas de la hija de Fernando son Ana y Micaela.
¿Quién es hija de Abel y quién, padre de Ana?
A) Micaela - César
B) Micaela - Marcos
C) Camila - Marcos
D) Camila - César
E) Fiona - César
PREGUNTA 25 :
Una urna contiene ocho bolos idénticos numerados desde el 2 hasta el 9, todos con numeración diferente. ¿Cuántos bolos como mínimo se debe extraer al azar para tener con certeza, entre los bolos extraídos, tres bolos cuya numeración sea consecutiva?
A) 5
B) 6
C) 7
D) 4
E) 3
PREGUNTA 26 :
La final de un torneo de fulbito la disputan los equipos M, N, P y Q, jugando todos contra todos, una sola rueda. En la tabla, se muestra algunos datos de los partidos ganados (PG), partidos empatados (PE), partidos perdidos (PP), goles a favor (GF), goles en contra (GC) y el puntaje final. Si por partido ganado se considera tres puntos; por partido empatado, un punto y por partido perdido, cero puntos, ¿cuál fue el resultado del partido entre N vs. Q, en ese orden?
A) 2 - 3
B) 2 - 1
C) 2 - 0
D) 1 - 0
E) 1 - 2
PREGUNTA 27 :
La figura representa una lámina triangular cuyos vértices son los puntos A, B y C, ubicada en el primer cuadrante del plano cartesiano. Si los lados de los cuadraditos de la cuadrícula miden 1 cm y se construye la figura asimétrica de dicha lámina respecto al eje X obteniendo un nuevo triángulo ΔA’B’C’ en el cuarto cuadrante, calcule la distancia máxima, en centímetros, de uno de los vértices del triángulo ΔA’B’C’ al origen O del sistema de coordenadas.
A) √17
B) 3√5
C) 3√2
D) √5
E) 2√5
PREGUNTA 28 :
En un circo, actúa un malabarista que hace uso de una bicicleta cuya rueda trasera tiene un radio que mide 24 cm y el radio de la rueda delantera mide 36 cm. Si en un acto de su función, la rueda delantera dio 100 vueltas menos que la trasera al desplazarse por el escenario, halle la longitud que recorrió la bicicleta en su desplazamiento.
A) 144𝛑 m
B) 140𝛑 m
C) 124𝛑 m
D) 146𝛑 m
E) 150𝛑 m
PREGUNTA 29 :
Manuel tiene fichas de madera de tipo 1, tipo 2, tipo 3, como se muestra en la figura. Las fichas de tipo 1 y tipo 2 están formadas por cuatro cuadraditos cuyos lados miden 3 cm y la ficha de tipo 3 es un cuadradito cuyos lados miden 3 cm. Con dichas fichas, colocándolas sobre una mesa plana, adyacentes y sin superponerlas, forma diversas figuras, utilizando siempre por lo menos dos fichas de cada tipo, y se propone formar un rectángulo de menor perímetro. ¿Cuál sería el perímetro del rectángulo a formar?
A) 66 cm
B) 54 cm
C) 48 cm
D) 56 cm
E) 44 cm
PREGUNTA 30 :
José María Arguedas Altamirano nació el 18 de enero de 1911, en Andahuaylas. Fue antropólogo, etnólogo y autor de novelas y cuentos que lo llevaron a ser considerado uno de los tres grandes representantes de la narrativa indigenista en el Perú. ¿Qué día de la semana nació?
A) martes
B) sábado
C) miércoles
D) lunes
E) jueves
CLAVES DE RM : 16)D 17)B 18)D 19)A 20)C 21)B 22)E 23)D 24)B 25)C 26)D 27)C 28)A 29)B 30)C
PREGUNTA 1 :
Si fueran 10 horas más tarde de lo que es, faltaría, para acabar el día, el doble del tiempo que habría transcurrido hasta hace 5 horas. ¿Qué hora es?
A) 9 h
B) 10 h
C) 7 h
D) 8 h
E) 6 h
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 2 :
En la siguiente secuencia de figuras, calcule la suma de todos los elementos de la figura 11.
A) 2626
B) 2642
C) 2602
D) 2862
E) 2662
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 3 :
En la figura adjunta, recorriendo solamente los segmentos hacia arriba, a la izquierda y en diagonales hacia arriba, ¿cuántas rutas diferentes existen para ir desde el punto B hasta el punto A?
A) 63
B) 39
C) 48
D) 52
D) 47
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 4 :
Una institución educativa realizó una encuesta a sus 300 estudiantes sobre su deporte favorito, y obtuvo el siguiente resultado: 120 estudiantes prefieren solo fútbol; 96 estudiantes eligieron solo ajedrez; y el resto de estudiantes prefiere vóley. Además, ninguno de los estudiantes prefiere dos o más deportes. Para representar los resultados, se utiliza una gráfica de barras, donde su longitud es proporcional a las cantidades de estudiantes encuestados que prefieren un deporte. Si la longitud de la barra que corresponde a la cantidad de estudiantes que prefieren ajedrez mide 8 cm, halle la diferencia positiva de las longitudes de las otras dos barras que corresponden a la cantidad de estudiantes encuestados que prefieren los otros deportes.
A) 2,7 cm
B) 4 cm
C) 1,5 cm
D) 2 cm
E) 3 cm
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 5 :
Con las propinas que recibió, Marita logró reunir 100 soles en monedas de 20 y 50 céntimos y monedas de 1; 2 y 5 soles. ¿Cuál es la máxima cantidad de monedas que puede tener Marita si recibió, al menos, cinco monedas de cada denominación?
A) 294
B) 306
C) 298
D) 308
B) 360
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 6 :
En un restaurante, para optimizar el espacio, se ubica una mesa de forma hexagonal regular con seis asientos simétricamente ubicados. Cinco amigos que llegan a cenar se distribuyen de la siguiente manera: Abel se sienta junto a María, José se sienta junto y a la izquierda de Inés. Entre Inés y María, y junto a ellas, se sienta Andrés.
Señale la afirmación verdadera.
A) María y José se sientan juntos.
B) A la izquierda de Abel, está el asiento vacío.
C) María se sienta junto a Inés.
D) A la izquierda de José, está el asiento vacío.
E) A la derecha de José, está el asiento vacío.
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 7 :
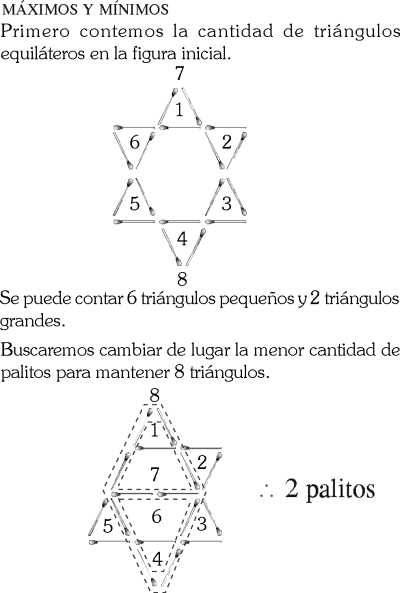
En la figura, hay dieciocho cerillos de igual longitud que forman triángulos equiláteros. ¿Cuántos cerillos podemos cambiar de posición, como mínimo, manteniendo el mismo número de triángulos equiláteros de la figura?
A) 4
B) 2
C) 5
D) 3
E) 8
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 8 :
Cinco amigas ingresaron a un concierto, pero se sabe que solo una de ellas no ha pagado su entrada. El equipo de seguridad de los organizadores las detiene e interroga. Durante el interrogatorio, el equipo de seguridad deduce que dos de ellas mienten y las demás dicen la verdad.
Ante las preguntas que les fueron formuladas, ellas respondieron lo siguiente:
• Ana: Diana no pagó su entrada.
• Beatriz: Yo pagué mi entrada.
• Carla: Esther pagó su entrada.
• Diana: Ana miente.
• Esther: Beatriz dice la verdad.
¿Quién no pagó su entrada?
A) Beatriz
B) Esther
C) Carla
D) Diana
E) Ana
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 9 :
La siguiente figura representa una red de caminos. Recorriendo solamente las líneas, ¿cuántas rutas diferentes existen para ir desde el punto A hacia el punto B sin pasar dos veces por el mismo punto?
A) 12
B) 30
C) 28
D) 24
E) 16
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 10 :
Un comerciante dispone de 100 kg de azúcar y tres pesas, la primera de 4 kg, la segunda de 7 kg y la tercera de 13 kg. ¿Cuántas pesadas deberá realizar, como mínimo, para vender 18 kg de azúcar?
A) 2
B) 1
C) 3
D) 4
E) 5
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 11 :
Cinco hermanos, Arón, Raúl, Juvenal, Liberato y Germán, que tienen 21 ; 23 ; 25 ; 27 y 28 años de edad, respectivamente, son aficionados al motociclismo y, en una semana, cada hermano entrena un solo día, en la única motocicleta que tiene la familia. Uno de ellos entrena lunes; otro, martes; otro, miércoles; otro, jueves, y otro, viernes. Además, se sabe lo siguiente:
• Arón solo puede entrenar a partir del jueves.
• Raúl entrena un día después de Liberato.
• Juvenal entrena el viernes.
• Ni Liberato ni Raúl pueden entrenar los miércoles.
¿Cuánto suman, en años, las edades de los hermanos que entrenan lunes y miércoles?
A) 55
B) 52
C) 50
D) 48
E) 36
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 12 :
En un campo petrolero hay 20 pozos. Cada pozo produce 200 barriles diarios de petróleo. Se sabe que, por cada nuevo pozo perforado, la producción diaria de cada pozo disminuirá en 5 barriles. ¿Cuántos pozos debería haber en este campo con el fin de maximizar la producción diaria de barriles de petróleo?
A) 25
B) 10
C) 30
D) 40
E) 36
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 13 :
Luciana tiene un saco con 60 kilogramos de azúcar y desea retirar 5 kilogramos de él. Si Luciana dispone de una balanza de dos platillos y una pesa de dos kilogramos, ¿cuántas pesadas, como mínimo, tendrá que realizar para obtener los 5 kilogramos de azúcar?
A) 1
B) 4
C) 5
D) 3
E) 2
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 14 :
En una urna que solo contiene bolas, hay 10 bolas rojas, 10 azules, 10 verdes y 10 amarillas. ¿Cuál es el menor número de bolas que se debe extraer, al azar, para obtener con certeza 4 bolas del mismo color?
A) 4
B) 10
C) 5
D) 12
E) 13
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 15 :
La municipalidad de Santiago de Surco usó material reciclable para sus adornos navideños. En uno de sus adornos usó botellas idénticas: sobre la pared de un edificio, armaron un gran árbol navideño en forma triangular usando botellas de plástico en desuso, como se muestra en la figura. Si en la base hay 100 pares de botellas, ¿cuántas botellas en total se utilizaron para construir dicho árbol?
A) 10 000
B) 5050
C) 10100
D) 5500
E) 36050
RESOLUCIÓN :
Rpta. : "C"
SEGUNDA PRUEBA
PREGUNTA 16 :
César se encuentra mal de salud y acude a una clínica; el médico le receta los siguientes medicamentos: 4 cápsulas del tipo A cada ocho horas y 2 cápsulas del tipo B cada doce horas. El médico le dice que el tratamiento acabará cuando haya tomado 76 cápsulas en total. Si empieza el tratamiento tomando ambos tipos de cápsulas (4 del tipo A y 2 del tipo B) el jueves 4 de agosto a las 10 de la mañana, ¿en qué fecha y hora terminará el tratamiento?
A) Lunes 8 de agosto y 6:00 p. m.
B) Martes 9 de agosto y 10:00 p. m.
C) Lunes 8 de agosto y 10:00 p. m.
D) Domingo 7 de agosto y 10:00 p. m.
E) Martes 9 de agosto y 6:00 p. m.
PREGUNTA 17 :
La figura representa una estructura hecha de alambre. ¿De cuántas formas distintas recorriendo solo por el alambre puede ir una hormiga del punto A al punto B sin pasar dos veces por el mismo tramo?
A) 60
B) 36
C) 50
D) 46
E) 48
PREGUNTA 18 :
Miguel escribe un algoritmo usando el siguiente diagrama de flujo que genera números enteros, de tal manera que los números pares de dos cifras impresos por el algoritmo serán las claves para sus archivos personales. Si Miguel ingresa el número 27, ¿cuántas claves distintas, impresas por el algoritmo, tendrá a su disposición?
A) 23
B) 24
C) 26
D) 25
E) 22
PREGUNTA 19 :
Federico Villarreal nació el 30 de agosto de 1850 en Túcume, departamento de Lambayeque (Perú). ¿Qué día de la semana nació Federico Villarreal?
A) Lunes
B) Martes
C) Viernes
D) Miércoles
E) Jueves
PREGUNTA 20 :
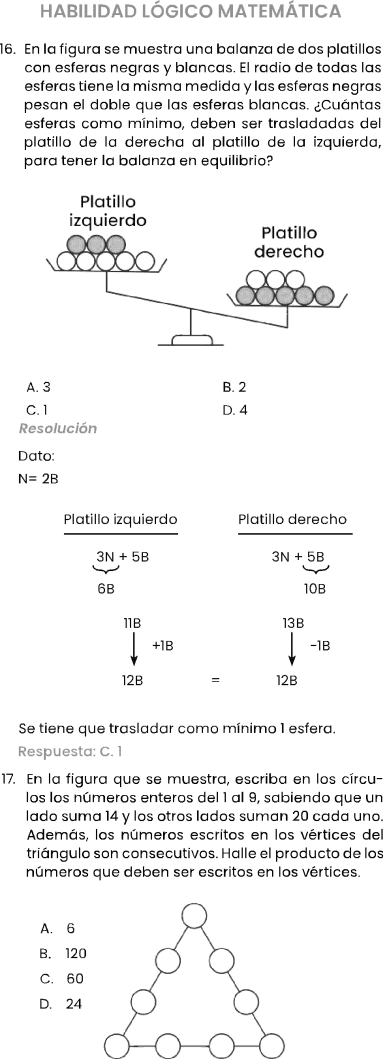
La figura muestra una balanza que no está en equilibrio. Si el peso de una canica negra es igual al doble del peso de una canica blanca, para equilibrar la balanza, ¿cuántas canicas negras y cuántas blancas, respectivamente, se deben trasladar del platillo B al platillo A?
A) 3 y 1
B) 3 y 2
C) 5 y 1
D) 4 y 1
E) 4 y 2
PREGUNTA 21 :
Un vendedor tiene un saco con 47 kg de azúcar y recibe un pedido de 7kg. Cuenta con una balanza de dos platillos y solo una pesa de 3kg. ¿Cuántas pesadas tendrá que realizar, como mínimo, para atender el pedido?
A) 6
B) 2
C) 4
D) 5
E) 3
PREGUNTA 22 :
Sergio y Jesús parten simultáneamente de un puerto en dos botes con velocidades constantes para realizar pesca deportiva. Sergio parte en la dirección S60°O y Jesús en la dirección NO. Transcurridas cinco horas, Jesús se encuentro exactamente al norte de Sergio a 70(1+√3) km de distancia. Calcule la velocidad del bote de Sergio.
A) 28√2 km/h
B) 28 km/h
C) 26 km/h
D) 20 km/h
E) 15√2 km/h
PREGUNTA 23 :
La figura muestra una estructura de alambre formada por líneas horizontales, en la que se aprecia un cuadrado de vértices ABCD cuyos lados miden 30 cm, donde AC es su diagonal y da lugar a varios triángulos isósceles. Las longitudes en la figura están en centímetros. Determine la menor longitud que debe recorrer una hormiga que se encuentra en el punto A para pasar por el toda la estructura de alambre y terminar en el punto M.
A) 10(23+14√2) cm
B) 10(25+13√2) cm
C) 70(3+2√2) cm
D) 70(3+√2) cm
E) 10(21+2√2) cm
PREGUNTA 24 :
Tres parejas de esposos deciden ir al teatro y compran seis boletos numerados con seis números consecutivos.
La numeración de los boletos se corresponde con la numeración de las únicas seis butacas que se encuentran en una fila. Además, se sabe lo siguiente:
• Dos varones o dos mujeres no están sentados juntos.
• Roberto no se sentó en uno de los extremos y saludó a Miguel.
• Karla está sentada a la izquierda de todos los varones.
• Jairo está sentado junto a su esposa Sofía, pero no al lado de Pamela.
• Roberto está junto y al lado izquierdo de su esposa.
Indique qué afirmación es verdadera.
A) Pamela está sentada a la derecha de Miguel.
B) Roberto está sentado a la izquierda de Miguel.
C) Karla está sentada junto a Miguel.
D) Jairo está sentado junto a Pamela.
E) Roberto está sentado a la derecha de Pamela.
PREGUNTA 25 :
La figura representa un disco cuyo centro es el punto O y su radio OM mide 24 cm. Este disco avanza girando en el sentido que indica la flecha. ¿Cuántas vueltas dará el disco hasta el instante en que el punto M toque la superficie por sexta vez?
A) 17/2
B) 17/6
C) 17/3
D)16/3
E) 13/6
PREGUNTA 26 :
Un agricultor y su hijo se dedican a la siembra de cacao en las orillas del río Ucayali. Para trasladar un saco de 70 kg de cacao y otro de 60 kg a la otra orilla, disponen de una pequeña canoa que soporta un máximo de 100 kg. El agricultor pesa 70 kg y su hijo, 30 kg, ambos saben remar y tienen que cruzar a la otra orilla. ¿Cuántos viajes de una orilla a otra tendrán que realizar, como mínimo, en la canoa para trasladar los dos sacos de cacao y que ambos crucen el río?
A) 6
B) 4
C) 3
D) 5
E) 7
PREGUNTA 27 :
Un escultor recibe un plano donde aparecen la vista frontal, perfil derecho y horizontal de un sólido de madera, como muestra la figura. Si el escultor logró construir dicho adorno de volumen máximo, ¿cuántas caras tiene el adorno?
A) 10
B) 11
C) 12
D) 13
E) 14
PREGUNTA 28 :
Daniel y Pedro son dos amigos mitómanos que estudian en la universidad. Daniel miente los jueves, viernes y sábado, y los otros días dice la verdad. Pedro miente los domingos, lunes y martes, y los otros días dice la verdad. Un día se encuentran en la-universidad y sostuvieron el siguiente diálogo:
Daniel: «Hola ¡ayer yo mentí al decir que estudié matemática!»
Pedro: «Hola ¡ayer yo también mentí al decir que estudié matemática!»
¿Qué día de la semana fue el día siguiente del día del encuentro?
A) Lunes
B) Domingo
C) Sábado
D) Viernes
E) Martes
PREGUNTA 29 :
En el sistema de coordenadas cartesianas que se muestra, se tiene un triángulo con vértices en los puntos A(3;2), B(7;6) y C(9;4). Se construye el triángulo simétrico al triángulo de vértices ABC tomando como punto de simetría el punto O y se obtiene el triángulo A'B'C'. Calcule la suma de las abscisas de las coordenadas del triángulo determinado por los puntos medios de los lados del triángulo A'B'C'.
A) 19
B) –16
C) –19
D) 10
E) 15
PREGUNTA 30 :
Arpones, Barlovento y Catenaria fueron los tres equipos de fútbol que se formaron en el taller de verano en la Villa Deportiva Nacional (VIDENA). Se enfrentaron en un torneo en el que jugaron todos contra todos una sola vez, donde Arpones logró anotar tres goles en el torneo, Barlovento anotó dos goles y solo tuvo victorias, Catenaria alcanzó un empate. ¿Cuál es la diferencia del número total de goles en el partido que terminó empatado con la suma de la cantidad total de goles de los partidos entre Barlovento vs Catenaria y Arpones vs Barlovento?
A) 1
B) 3
C) 2
D) 4
E) 0
CLAVES DE RM : 16)C 17)E 18)E 19)C 20)D 21)C 22)B 23)C 24)B 25)C 26)D 27)C 28)A 29)C 30)D