GEOMETRÍA DE EXAMEN ADMISIÓN UNIVERSIDAD PRUEBA AUTO EVALUACIÓN CON CLAVES RESPUESTAS

PREGUNTA 1:

En una recta se ubican los puntos consecutivos: L, O, P, E y Z.

Tal que LO=2(OP) y EZ = 3(PE).

Si EZ+LP=36 cm, halle OE.

A) 15 cm

B) 12 cm

C) 10 cm

D) 9 cm

E) 16 cm

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 2:

Calcule la medida del ángulo “x” del siguiente gráfico, siendo L1//L2

A) 15º

B) 30º

C) 45º

D) 60º

E) 75º

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 3:

Si el ángulo externo de un polígono regular mide 36º, calcule el mayor número de diagonales que se puede trazar:

A) 20

B) 28

C) 35

D) 44

E) 54

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 4:

En la figura, calcule el valor de “X”:

A) 59º

B) 60º

C) 45º

D) 36º

E) 10º

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 5:

Las diagonales de un rombo miden 12 y 16 cm. Halle la distancia que hay entre dos lados opuestos:

A) 9,4 cm

B) 9,8 cm

C) 9,7 cm

D) 9,6 cm

E) 9,5 cm

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 6:

Halle el área del triángulo rectángulo cuya hipotenusa se encuentra dividida en 5 y 12 cm y mantiene una circunferencia inscrita de radio “r”

A) 40 cm²

B) 50 cm²

C) 60 cm²

D) 70 cm²

E) 80 cm²

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 7 :

En la figura adjunta: si la medida del segmento AB es 8 cm y la medida del radio OM es 5 cm, entonces el área del rectángulo ABCD es

A) 40 cm²

B) 48 cm²

C) 56 cm²

D) 64 cm²

E) 72 cm²

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 8:

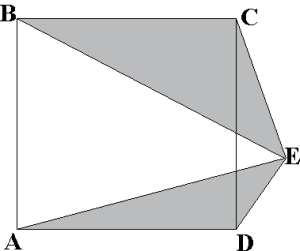
La figura ABCD es un cuadrado de lado 5m. Calcule el área de la región sombreada.

A) 12,5 m²

B) 9,5 m²

C) 15,5 m²

D) 8,5 m²

E) 5,5 m²

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 9:

En la figura mostrada, halle el área de la región sombreada, si “O” es el centro:

A) 30𝜋 cm²

B) 25𝜋 cm²

C) 15𝜋 cm²

D) 40𝜋 cm²

E) 24𝜋 cm²

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 10:

Los catetos del triángulo rectángulo DBE miden “a” y “b”. si AD = DE = EC. Halle el área del triángulo ABC.

A) 3 𝑎. 𝑏

B) 2 𝑎. 𝑏

C) 1,5𝑎. 𝑏

D) 2/3 𝑎. 𝑏

E) 𝑎. 𝑏

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 11:

En la figura mostrada, el área de la región triangular ABC es 42 m². Si PC=2BP y AQ=2QC, halle el área de la región mostrada.

A) 2m²

B) 4m²

C) 3m²

D) 2,5m²

E) 3,5m²

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 12:

En el gráfico, calcule “x”

A) 5

B) 4

C) 3

D) 2

E) 1

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 13:

En el gráfico, AB =6m y BC =8m; D y E son puntos de tangencia. Halle el área de la región sombreada

A) 10m²

B) 16m²

C) 8m²

D) 6m²

E) 12m²

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 14:

Un acuarista elaboró un novedosos acuario, cuya base es un hexágono de 10 cm de arista, y una altura de 15 cm. Halle la cantidad de vidrio que utilizó:

A) (900 + 150√3) cm²

B) 800 cm²

C) 1800 cm²

D) 1000 cm²

E) 700√3 cm²

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 15:

En la figura dada, halle la ecuación de la recta L2 que pasa por el punto A(2;6) y es perpendicular a la recta L1.

A) 4x + 3y= 26

B) 3x + 4y = 26

C) 4x − 3y = 23

D) 3x − 4y = 23

E) 5x − y = 26

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 16 :

¿ Cuál es la ecuación de la recta que pasa por el origen y es perpendicular a la recta

3x–2y = 6 ?

A) 2x + 3y = 0

B) 3x + 2y = 1

C) 2x – 3y = 6

D) 3x + 4y = 2

E) 2x – 3y = 4

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 17 :

En el gráfico, ABCD es un rectángulo donde AB=3 y BC=4. Calcula el área de la región sombreada.

A) 13,5

B) 14,5

C) 15,5

D) 18,5

E) 16,5

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 18 :

Se tiene el paralelogramo ABCD, AB=6, BC=10, una de las alturas es 8. Calcule la otra altura.

A) 1,5

B) 2,5

C) 2

D) 3

E) 4

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 19 :

En el gráfico calcule x

A) 55º

B) 85º

C) 65º

D) 45º

E) 75º

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 20 :

Se tiene una circunferencia de radio T, si se duplica su radio, la longitud de la circunferencia mayor es x veces la longitud de la circunferencia menor.

Calcule x

A) 3

B) 2,5

C) 1

D) 4

E) 2

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 21 :

Sobre un segmento AB se ubica el punto medio C y sobre BC se ubica el punto D, desde C, D y B se levantan perpendicularmente CF, DG y BH de 10 m de longitud cada uno. Si el área de la región AFGD es igual al área de la región DGHB, calcula CD si AB=12 m.

A) 1,5

B) 2

C) 2,5

D) 3,5

E) 3

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 22 :

En el gráfico mostrado, PA=9, RG=7 y PG=8.

A) 5

B) 5,5

C) 6

D) 6,5

E) 9

RESOLUCIÓN :

Relaciones métricas en triángulo rectángulo

Por teorema Pitágoras

R²=9²+(8 – x)²

⇒ R²=72+x²

⇒ 9²+(8 – x)²= 7²+x² ⇒ x=6

Rpta. : "C"

PREGUNTA 23 :

A) 30°

B) 45°

C) 75°

D) 80°

E) 60°

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 24 :

Del grafico; calcule el perímetro de la región sombreada ABCD: Cuando; M, N, P y Q son puntos medios.

A) 4 + 𝛑

B) 4 + 𝛑/2

C) 4 + 2𝛑

D) 4 + 3𝛑/2

E) 6 + 𝛑

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 25 :

Se tienen cuatro ángulos consecutivos AOB, BOC, COD y DOE tal que A, O, E son colineales, se sabe que los cuatro ángulos se encuentran en progresión aritmética y además la medida del ángulo mayor es el doble de la medida del ángulo menor. Calcule la diferencia de los dos ángulos intermedios en medida.

A) 5º

B) 8º

C) 10º

D) 12º

E) 18°

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 26 :

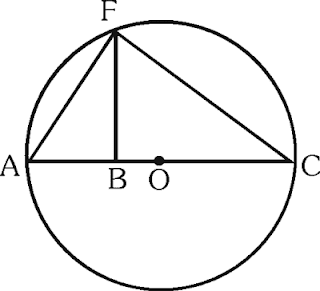
Del gráfico; el diámetro, AC mide 32μ, BO=4. Si FB⊥AC, calcule el perímetro de la región triangular AFC.

A) 4√6 + 5√10 + 32

B) 8√6 + 7√10 + 32

C) 8√6 + 8√10 + 32

D) 5√3 + 7√8 + 36

E) 8√6 + 5√10 + 32

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 27 :

Del gráfico, AEFD es un cuadrado, ABCD es un rectángulo, M es punto medio y AM = 1. Calcule el área de la región EBCF.

A) 4 u²

B) 6 u²

C) 9 u²

D) 10 u²

E) 8 u²

RESOLUCIÓN :

Rpta. : "E"

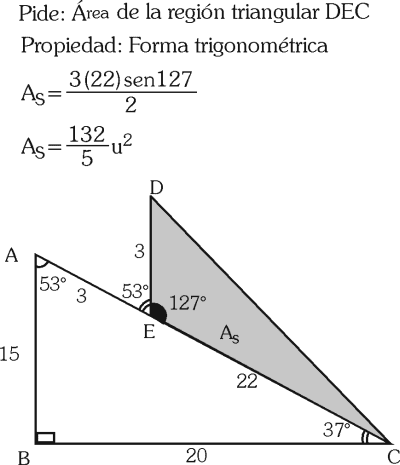
PREGUNTA 28 :

A) 120/7 u²

B) 132/5 u²

C) 140/9 u²

D) 135/8 u²

E) 187/7 u²

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 29 :

Del gráfico, O y O₁ son centros; A, B, C, D y E son puntos de tangencia. Calcule el área de la región sombreada.

A) 12√2 u²

B) 18√2 u²

C) 22√2 u²

D) 24√2 u²

E) 32√2 u²

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 30 :

A) √5 – √(14/3)

B) √5 – √5/3

C) √7 – √(14/3)

D) √6 – √(14/3)

E) 5 – √5/7

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 31 :

Calcule el área de la región sombreada si “O” y “O1” son centros. Si AB = 2u , EF = 1u

A) (√2 – 𝛑/6) u²

B) (√7 – 𝛑/3) u²

C) (√2 – 𝛑/5)/5 u²

D) (√3 – 𝛑/6)/4 u²

E) (√5 – 𝛑/7) u²

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 32 :

En un prisma hexagonal regular ABCDEF-GHIJKL, se inscribe una pirámide regular tal que su base coincide con la base ABCDEF y su vértice coincide con el centro de la base superior. La arista lateral de la pirámide mide 20 u y forma con el plano de la base un ángulo cuya medida es 60º. Calcule el volumen del Prisma.

A) 3 500 u³

B) 4 200 u³

C) 4 000 u³

D) 5 200 u³

E) 4 500 u³

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 33 :

A) 2

B) 3

C) 4

D) 5

E) 2,5

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 34 :

En una circunferencia de radio cuatro, se inscribe un cuadrado, luego se construye exteriormente los triángulos equiláteros formándose un octógono del cual nos piden el área.

A) 18(√3 + 2)

B) 32(√2 + 1)

C) 16(√2 + 1)

D) 32(√5 + 1)

E) 32(√3 + 1)

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 35 :

Se tiene un terreno PQR, QR=8, QP=6, PR=10, luego se levanta las perpendiculares ⊥PN, ⊥QS y ⊥RT, PN=3, QS=10 y RT=5. Calcule el área de la malla que limita el terreno formado por las perpendiculares.

A) 139

B) 143

C) 131

D) 157

E) 128

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 36 :

En un triángulo isósceles de base AC=1, se trazan las medianas que parten de los extremos de las bases y son perpendiculares. Calcula el área de la región triangular.

A) 1/2

B) 1/3

C) 1/4

D) 3/4

E) 2/3

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 37 :

En un triángulo equilátero ABC de lado 6√2, se ubican los puntos P y Q en AB y BC, respectivamente. Si PQ es paralelo a AC y las regiones determinadas son equivalentes, calcula PQ.

A) 9

B) 3√2

C) 7

D) 8

E) 6

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 38 :

En el gráfico, calcula el área de la región sombreada.

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 39 :

En el triángulo, ABCD es un paralelogramo, BE=3 y EC=4. Calcula EC/AD

A) 3/5

B) 4/5

C) 4/3

D) 4/7

E) 1/8

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 40 :

En el gráfico calcule x

A) 118º

B) 122º

C) 140º

D) 134º

E) 124º

RESOLUCIÓN :

Líneas notables –Triángulos

Por propiedad: x=90° + 68°/2

⇒ x=124º

Rpta. : "E"

PREGUNTA 41 :

Se tienen, sobre una recta, los puntos consecutivos A, B, C y D, tal que

BC=5 y 7AD – BC=2AC+7BD.

Calcule AB.

A) 2

B) 3

C) 4

D) 1

E) 2,5

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 42 :

En un cuadrado ABCD, se construye internamente el triángulo equilátero APD. Calcule la medida del ángulo determinado por los segmentos BD y AP.

A) 50º

B) 90º

C) 45º

D) 80º

E) 75º

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 43 :

En un triángulo rectángulo, la longitud de uno de sus catetos es BC=√2. Si el otro cateto tiene por longitud la tercera parte de la hipotenusa, calcule la longitud de la hipotenusa.

A) 0,5

B) 1

C) 1,5

D) 2

E) 3

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 44 :

En un paralelogramo de lados 6 y 16, la distancia entre los lados menores es 8. Calcule la distancia entre los lados mayores.

A) 1

B) 3

C) 5

D) 4

E) 6

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 45 :

En un paralelogramo ABCD, AB=5 y BC=16. Si P es el punto de intersección de las bisectrices interiores de los ángulos B y C, calcule la distancia del punto P al punto medio del lado BC.

A) 2

B) 4

C) 6

D) 1

E) 8

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 46 :

En un triángulo de lados 6 y 12 se inscribe un rombo, calcule el lado de dicho rombo.

A) 1

B) 2

C) 3

D) 4

E) 6

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 47 :

Se tienen los segmentos colineales y consecutivos AM y MB, tal que el segmento MN es perpendicular a AB, tal que NB=AB=5 y MN=2(AM). Calcule el área de la región triangular MNB.

A) 4 u²

B) 5 u²

C) 6 u²

D) 8 u²

E) 7 u²

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 48 :

En el gráfico, AB=BL=LP=PC y AD=DL=LQ=QC. Calcule: x+y

A) 50º

B) 30º

C) 40º

D) 60º

E) 77°

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 49 :

En un triángulo rectángulo ABC se prolonga la hipotenusa hasta un punto D.

Si BC=CD=7 y AD=32, calcule la altura relativa a la hipotenusa.

A) 6,25

B) 6,72

C) 5,12

D) 5,25

E) 7,24

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 50 :

Se tienen dos triángulos equiláteros, uno inscrito y el otro circunscrito a una misma circunferencia. Si el área de la región determinada por las dos regiones triangulares es 9√3 u², calcule la longitud de la circunferencia.

A) 3𝛑

B) 2𝛑

C) 9𝛑

D) 6𝛑

E) 4𝛑

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 51 :

Se tienen dos circunferencias circunscritas a dos hexágonos regulares. Si sus radios miden 4 y 8, calcule la relación de áreas de las regiones determinadas entre las circunferencias y sus polígonos regulares inscritos.

A) 1/4

B) 1/2

C) 1/8

D) 1/6

E) 2/9

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 52 :

Del gráfico, calcule el área sombreada, si PQ=2, R=√2 (T: punto de tangencia).

A) 2√2 – 2 – 𝛑/2

B) 2√2 – 1 – 𝛑/2

C) 2√2 + 1 – 𝛑/2

D) 2√2 – 1 – 𝛑/2

E) √2 + 1 – 𝛑/2

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 53 :

En un cono de 8 cm de altura y de radio 5, calcule la generatriz del cilindro inscrito en el cono si el área lateral del cilindro es 20π u².

A) 2

B) 4

C) 6

D) 8

E) 9

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 54 :

En un cubo de arena se hace una excavación de una esfera cuyo diámetro es igual a la arista del cubo y el radio de la esfera es 3 cm. Calcule el volumen restante de la arena.

A) 12(5 – π) u³

B) 24(6 – π) u³

C) 30(6 – π) u³

D) 26(5 – π) u³

E) 36(6 – π) u³

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 55 :

En un prisma hexagonal regular, la arista lateral es el doble de su arista básica y el volumen del prisma es 24√3 u³. Calcule el área lateral del prisma.

A) 36 u²

B) 64 u²

C) 40 u²

D) 50 u²

E) 48 u²

RESOLUCIÓN :