GEOMETRÍA UNI PREGUNTAS RESUELTAS DE EXAMEN ADMISIÓN UNIVERSIDAD

PREGUNTA 1 : 

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 2 : 

Al cortarse dos cuerdas de una misma circunferencia perpendicularmente, una de ellas queda dividida en segmentos de 3 y 4 unidades y la otra en segmentos de 6 y 2 unidades. Determine el diámetro de la circunferencia. 

A)√87 

B)√73 

C)√68 

D)√65 

E)√63 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 3 : 

La figura muestra tres semicircunferencias y la longitud de la circunferencia mayor es 10π u. Si AB=√24 u, siendo AB tangente a las semicircunferencias interiores, calcule la longitud (en u) de la circunferencia menor.

A) 2π 

B) 3π 

C) 4π 

D) 5π 

E) 6π 

RESOLUCIÓN :

Rpta. : "C" 

PREGUNTA 4 : 

Para tres circunferencias tangentes (exteriormente) dos a dos, la suma de sus radios es 10 cm y el producto de los mismos es 40 cm³. Halle el área (en cm²) de la región triangular cuyos vértices son los centros de la circunferencia. 

A) 18 

B) 18,5 

C) 19 

D) 19,5 

E) 20 

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 5 : 

La figura muestra dos rectas alabeadas que forman un ángulo de 120°. Si la distancia entre las rectas es de 2√3 u y AB=BC=CD. 

Determine AD (en unidades u). 

A) 5√6 

B) 2√6 

C) 4√6 

D) 3√6 

E) √6 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 6 : 

Sean F, M, A y G puntos colineales y consecutivos, si FG= 27 , FM=x – y , MA=x+y , AG=2y – x. 

Calcule el mayor valor de x sabiendo que el valor de y es entero.

 A) 10 

B) 11 

C) 12 

D) 13 

E) 9 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 7 : 

Desde el centro de dos circunferencias concéntricas se trazan dos segmentos de rectas, el primero intersecta a las circunferencias en los puntos A y B, mientras que el segundo segmento las intersecta en los puntos C y D. Si los radios de las circunferencias están en la razón de 1 a 2 y la suma de sus cuadrados es 5. Determine el perímetro del trapecio circular, sabiendo que el ángulo que forman los segmentos es de 𝛑/3. 

A) 4+ 𝛑 

B) 1+ 𝛑 

C) 3+ 𝛑 

D) 4 – 𝛑 

E) 2+ 𝛑 

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 8 : 

Determine el número de diagonales de aquel polígono regular cuya suma de la medida de un ángulo interno con un ángulo externo es 10 veces sus número de lados. 

A) 115 

B) 145 

C) 135 

D) 125 

E) 155 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 9 :

Si ABCDEF es un hexágono regular y sobre AB se toma un punto R, que al ser unido con E determina un segmento secante a FC en el punto Q. Si, además, m∠FAQ=5θ y m ∠ERB=10θ , entonces el valor de θ es 

A) 12 

B) 10 

C) 14 

D) 16 

E) 8 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 10 : 

La superficie lateral de un prisma recto regular triangular es un rectángulo cuya diagonal mide 12 m y su altura 6√3 m. Calcule el área total del sólido (en m²). 

A) 38√3 

B) 39√3 

C) 40√3 

D) 41√3 

E) 42√3 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 11 : 

En la siguiente figura se muestran tres circunferencias tangentes dos a dos cuyos radios son 25 ; 4 y x. 

Determine el área de la región circular cuyo diámetro es 7√x . 

A) 26𝛑 

B) 25𝛑 

C) 36𝛑 

D) 16𝛑 

E) 20𝛑 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 12 : 

En el ángulo triedro trirectángulo O - ABC; si las áreas de las caras OAB, OBC y OAC miden

respectivamente S, 2S y 3S. Entonces el área de la región que determina un plano secante a las aristas y que pasa A, B y C es

A) 2S√2 

B) 3S√2 

C) S√14

D) 2S√3 

E) S√15

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 13 : 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 14 :

En la figura, determine x.

A) 17° 

B) 19° 

C) 18°

D) 16° 

E) 15°

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 15 : 

La figura representa un cubo de arista a cm. Calcule el área (en cm²) de la circunferencia que pasa por los puntos P, Q, R, S, T, U; teniendo en cuenta que son puntos medios de las aristas. 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 16 : 

En la figura, O y B son centros de los arcos respectivos. Además, los radios miden 10 u y 8 u. Determine MN (en unidades u). 

A) 8,6 

B) 5 

C) 6 

D) 6,9 

E) 6,8 

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 17 : 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 18 :

En la figura 

la medida del arco ANE es 184° y la medida del arco BFD es 124°. Halle la medida del arco BMD, en grados sexagesimales. 

A) 62 

B) 58 

C) 80 

D) 60 

E) 72 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 19 : 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 20 :

Un terreno tiene forma de un octógono regular y tiene un perímetro de 24(√2 −1) u. Determine la distancia desde el centro de la circunferencia circunscrita al terreno hacia un lado cualquiera del terreno (u). 

A) 1/2 

B) 5/2 

C) 3/2 

D) 7/2 

E) 9/2 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 21 : 

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 22 :

En la siguiente figura, determine el radio de la circunferencia más pequeña sabiendo que la distancia del punto O hacia la cuerda TC es de una unidad y los puntos A, B, T son puntos de tangencia. 

A) 5√2/7

B) 2√2/5

C) 8√2/5

D) 4√2/5

E) 6√2/5 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 23 : 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 24 :

El área total de un prisma regular hexagonal es el cuádruple de su área lateral. Determine el volumen (en cm³) del prisma si su lado de la base es 4 cm. 

A) 42 

B) 38 

C) 46 

D) 52 

E) 48 

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 25 : 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 26 : 

Dado un prisma oblicuo cuya sección recta es un triángulo de inradio 4 unidades y área lateral de 36 unidades cuadradas. Determine el volumen del prisma (en unidades cúbicas). 

A) 82 

B) 54 

C) 52 

D) 62 

E) 72 

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 27 : 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 28 :

¿Cuál de las siguientes proposiciones es verdadera? 

A) Si L₁ y L₂ son rectas paralelas y sean 𝛑₁ y 𝛑₂ planos que las contienen, respectivamente, de modo que se intersectan. Entonces la recta de intersección es paralela a L₁ y L₂. 

B) Si 2 planos son intersectados por un tercer plano, entonces las rectas de intersección son paralelas. 

C) Si los planos 𝛑₁ y 𝛑₂ son perpendiculares a las rectas L₁ y L₂, respectivamente, entonces dichos planos son secantes. 

D) Si L₁ y L₂ son rectas paralelas y sean 𝛑₁ y 𝛑₂ planos que las contienen, respectivamente, de modo que se intersectan. Entonces la recta de intersección es paralela solo a L₁ o solo a L₂. 

E) Si desde un punto exterior a un plano se traza una recta L perpendicular a una recta contenida en el plano, entonces la recta es perpendicular al plano. 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 29 : 

En un triángulo ABC, m∠BAC=2(m∠ACB) = 30°, si se traza la mediana BM, calcule m∠ABM. 

A) 75° 

B) 80° 

C) 90° 

D) 100° 

E) 105° 

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 30 : 

El cateto AB del triángulo rectángulo ABC se divide en 8 partes congruentes. Por los puntos de división se trazan 7 segmentos paralelos al cateto AC tal como se muestra en la figura. Si AC= 10 m, halle la suma (en m) de las longitudes de los 7 segmentos. 

A) 33 

B) 34 

C) 35 

D) 36 

E) 37 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 31 : 

En un cuadrilátero ABCD, las diagonales miden AC= 17 cm y BD= 15 cm; sea M punto medio de AC y F punto medio de BD; los ángulos interiores de B y D miden 90°. Calcule MF en cm. 

A) 2 

B) 3 

C) 4 

D) 5 

E) 6 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 32 : 

¿Cuál de las siguientes proposiciones es falsa? 

A) Solo en el tetraedro regular se puede inscribir, circunscribir y exinscribir esferas. 

B) En toda pirámide de A aristas, C caras y V vértices se cumple 

V=C=(A/2) +1 

C) El menor número de aristas que concurren en cada vértice, para todo poliedro convexo, es tres. 

D) En todo poliedro convexo de A aristas, C caras y V vértices se cumple 

C+V=A+ 2. 

E) En todo prisma de A aristas, C caras y V vértices se cumple 

C= (A/3) + 2

V = 3A/2

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 33 :

El volumen de un octaedro regular es de 9√2u³. Si se duplica la arista, determine el incremento del área total (u²). 

A) 50√3 

B) 52√3 

C) 54√3 

D) 56√3 

E) 58√3 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 34 : 

El punto A está a 8 m encima de un plano horizontal P, y el punto B se halla a 4 m encima del mismo plano. Si C es un punto del plano P tal que AC+BC es mínimo y el ángulo que forman la recta ↔CB con el plano P es 53°, entonces (en m) AC es 

A) 8 

B) 8,5 

C) 9 

D) 9,5 

E) 10 

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 35 : 

Las caras de un triedro equilátero de vértice V miden 60°. En una de sus aristas se considera un punto R de tal manera que VR= 2 cm. Por R pasa un plano perpendicular a VR que interseca a las otras aristas en S y T. Halle el área del triángulo RST (en cm²). 

A) 3√2 

B) 2√6 

C)√26 

D) 3√3 

E) 4√2 

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 36 : 

Sea el tetraedro regular de arista a, con a un entero positivo diferente de múltiplo de 3. Se unen los baricentros de las caras del tetraedro regular formando un tetraedro nuevo y así se repite el proceso n veces 

A) 8√3 

B) 16 

C) 8√6 

D) 16√2 

E) 32 

RESOLUCIÓN :

Rpta. : "B"

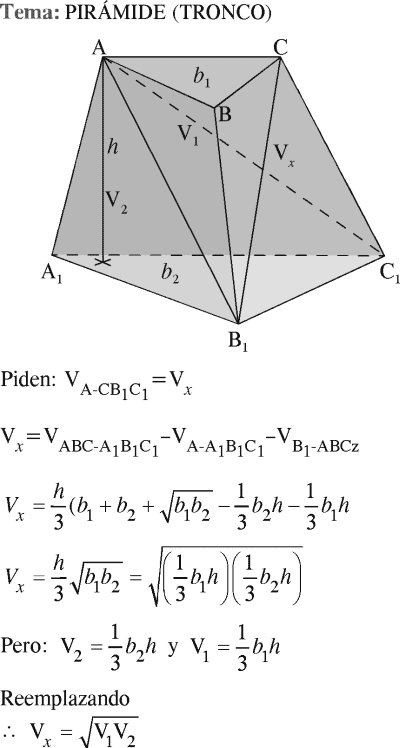
PREGUNTA 37 : 

En un tronco de pirámide ABC-A₁B₁C₁, los volúmenes de las pirámides B₁-ABC y A-A₁B₁C₁, miden V₁ y V₂ respectivamente. Determine el volumen de la pirámide A-CB₁C₁.

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 38 : 

El volumen de un cono de revolución es 36π cm³. Se inscribe un triángulo equilátero ABC en la base del cono. El triángulo ABC está circunscrito a una circunferencia cuyo círculo es base de un cilindro recto inscrito en el cono. Calcule el volumen del cilindro (en cm³). 

A) 27π/10 

B) 27π/8 

C) 27π/5 

D) 27π/2 

E) 27π 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 39 : 

Determine la longitud (en cm) del lado de un polígono regular inscrito en una circunferencia C de radio R cm si la longitud del lado de un polígono de doble número de lados inscrito en C es igual a R/2 cm. 

A) √15R/2  

B) √15R/3  

C) √15R/4  

D) √15R/5  

E) √15R/6  

RESOLUCIÓN :

Rpta. : "C"