FÍSICA UNI PREGUNTAS RESUELTAS DE EXAMEN ADMISIÓN UNIVERSIDAD
PREGUNTA 1 :
Se ha determinado que la magnitud F de una fuerza que actúa sobre un satélite que orbita la Tierra depende de la rapidez v del satélite, de la distancia media del satélite al centro de la Tierra R y de la masa m del satélite según la relación
Siendo K una constante adimensional, determine α+β+γ.
A) – 2
B) –1
C) 0
D) 1
E) 2
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 2 :
Un tren que viaja por unos rieles rectos con 54 km/h de rapidez constante atraviesa un túnel de 200m en 14s. Calcule, en s, el tiempo que el tren demora en atravesar el mismo túnel si ahora su velocidad es de 63 km/h.
A) 9
B) 18
C) 21
D) 15
E) 12
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 3 :
Suponga que la posición de un automóvil en el instante t está dada por la ecuación x(t)=5t²+3t +2 donde la posición x está en metros y t en segundos. Determine la variación de la velocidad, en m/s, entre los instantes t2=8 s y t1=3 s.
A) 75
B) 15
C) 25
D) 50
E) 100
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 4 :
En el dibujo, la tensión en la cuerda que une los bloques de masas 300 g y 400 g es de 2 N. Calcule aproximadamente, en N, la tensión en la cuerda que une los bloques de masas 200 g y 400 g.
A) 2,67
B) 1,67
C) 5,67
D) 3,67
E) 4,67
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 6 :
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 7 :
En el sistema mostrado, calcule aproximadamente la rapidez del pasajero en m/s, en el asiento de un columpio suspendido de un cable de 8,5 m que pende de un punto en un brazo a 4,0 m del eje de rotación.
(g=9,81 m/s²)
A) 4,4
B) 6,3
C) 8,0
D) 10,0
E) 14,0
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 8 :
Un rifle ubicado sobre el eje X dispara una bala con una rapidez de 457 m/s. Un blanco pequeño se ubica sobre el eje X a 45,7 m del origen de coordenadas. Calcule aproximadamente, en metros, la altura h a la que debe elevarse el rifle por encima del eje X, para que pueda dar en el blanco. Considere que el rifle siempre dispara horizontalmente. ( g=9,81 m/s²)
A) 0,01
B) 0,02
C) 0,03
D) 0,04
E) 0,05
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 9 :
Un cuerpo atado a una cuerda de 4 m de longitud se mueve en un círculo vertical (la aceleración de la gravedad vertical hacia abajo). Cuando la magnitud de la aceleración tangencial es 3/5 de la magnitud de la aceleración total, el cuerpo tiene una rapidez de 4 m/s. Calcule la magnitud de la aceleración total en m/s² en ese instante.
A) 8
B) 10
C) 4
D) 9
E) 5
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 10 :
Un bloque de masa m se desliza libremente hacia abajo sobre un plano inclinado en un ángulo α con respecto a la horizontal con una aceleración constante g/2 (donde g es la aceleración de la gravedad). Si el coeficiente de rozamiento entre el bloque y el plano es μ=0,5; calcule el ángulo α.
A) 30º
B) 37º
C) 43º
D) 53º
E) 60º
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 11 :
El extremo inferior de un resorte que cuelga del techo, que está unido a un cuerpo de 150 g, oscila con una frecuencia de 3 Hz. Si la velocidad máxima del cuerpo es de 0,9 m/s, calcule aproximadamente, en N, la fuerza máxima en el resorte.
A) 1,5
B) 5,5
C) 3,5
D) 4,5
E) 2,5
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 12 :
Una partícula de 2×10–21 kg de masa y carga 1,5×10–19 C, se encuentra en un campo eléctrico constante y homogéneo E=1000 V/m. La partícula se lanza desde un punto A, con una velocidad inicial perpendicular al campo eléctrico y de módulo igual a 20 m/s. Determine, en m/s, el módulo de la velocidad de la partícula al pasar por el punto B.
A) 30
B) 45
C) 35
D) 40
E) 25
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 13 :
El tiempo mínimo que demora una partícula que realiza un MAS en alcanzar la amplitud máxima desde la posición de equilibrio, es de 1,5 s. Si el módulo de la aceleración máxima es de 4 cm/s², calcule aproximadamente la rapidez máxima de la partícula en cm/s.
A) 2,82
B) 1,82
C) 4,82
D) 5,82
E) 3,82
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 14 :
En una catarata de 128 m de altura, el agua cae a razón de 1,4×10⁶ kg/s. Si la mitad de la energía potencial se convierte en energía eléctrica, calcule aproximadamente la potencia producida en W. ( g=9,81 m/s²)
A) 878,97
B) 878,97×103
C) 1757,94×103
D) 878,97×106
E) 1757,94×106
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 15 :
Una placa de aluminio de 5 mm de espesor se encuentra en contacto térmico con una placa de oro de 10 mm de espesor. La temperatura exterior de la placa de aluminio es de 20°C y la del oro es de 30°C. Calcule aproximadamente, en °C, la temperatura en la superficie de contacto, si la rapidez de transferencia de calor en ambas placas es la misma. Las conductividades térmicas del aluminio y del oro son 238 Wm–1K–1 y 314 Wm–1K–1, respectivamente.
A) 24
B) 27
C) 21
D) 26
E) 29
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 16 :
Desde lo alto de un edificio se deja caer un objeto el cual metros más abajo recorre una ventana de 2,2 m de alto en 0,28 s. Calcule aproximadamente la distancia (en m) desde el punto de donde se suelta hasta la parte más alta de la ventana. ( g=9,81 m/s²)
A) 1,52
B) 1,76
C) 1,82
D) 2,01
E) 2,14
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 17 :
Un buzo se sumerge en el océano alcanzando una presión manométrica de 1×10⁵ Pa. Determine aproximadamente la profundidad, en m, que logró descender.
Considere g=9,81 m/s² y la densidad del agua igual a 1015 kg/m³.
A) 25
B) 20
C) 15
D) 5
E) 10
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 18 :
En el circuito mostrado, calcule aproximadamente, en A, la corriente que fluye través de la resistencia R, que es igual a 5 Ω.
A) 0,27
B) 0,17
C) 0,47
D) 0,57
E) 0,77
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 19 :
Un tubo en forma de U contiene mercurio. Se vierte un líquido de densidad volumétrica igual a 0,85 g/cm³ en una rama del tubo, hasta llegar a una altura de 20 cm. Calcule, en mm, la altura en que se eleva el nivel inicial del mercurio en la otra rama.
Densidad volumétrica del mercurio: 13,6 g/cm³
A) 14,25
B) 10,25
C) 2,25
D) 6,25
E) 8,25
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 20 :
Se hace incidir desde el vacío un rayo de luz de 5×10–7 m de longitud de onda sobre la superficie plana de un cierto material en un ángulo de 60º con respecto a la normal a la superficie. Si el rayo refractado hace un ángulo de 30º con respecto de la normal, calcule, en m, la longitud de onda de este rayo en el interior del material.
A) 0,88×10–7
B) 1,38×10–7
C) 2,88×10–7
D) 3,48×10–7
E) 5,78×10–7
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 21 :
Una persona tiene una altura H desde los ojos hasta el suelo y observa un espejo adherido a una pared que se encuentra a una distancia d, como se observa en el dibujo. Si el espejo se encuentra a una altura h del suelo, la distancia x más cercana a la pared a la que se puede ubicar un objeto para que la persona lo vea reflejado en el espejo es:
Rpta. : "C"
PREGUNTA 22 :
En el circuito que se muestra, determine la magnitud de la resistencia r, de modo que la resistencia equivalente entre a y b sea igual a r/2.
A) 20
B) 5
C) 10
D) 15
E) 25
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 23 :
Un cuerpo se suelta sobre una rampa inclinada desde una altura de 20 cm. La rapidez con que llega al suelo es de 1m/s. Calcule aproximadamente el coeficiente de fricción cinético entre el cuerpo y la rampa. El ángulo de inclinación es de 37°.
(g= 9,81 m/s²).
A) 0,56
B) 0,61
C) 0,65
D) 0,75
E) 0,98
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 24 :
Una partícula electrizada ingresa en la dirección mostrada en la figura con rapidez de 2×10⁴ m/s a una zona donde se tiene un campo compuesto eléctrico y magnético. Si el campo magnético es B=0,05T y la partícula sigue una trayectoria rectilínea, encuentre (en kN/C) la intensidad del campo eléctrico E.
A) 1
B) 2
C) 3
D) 4
E) 5
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 25 :
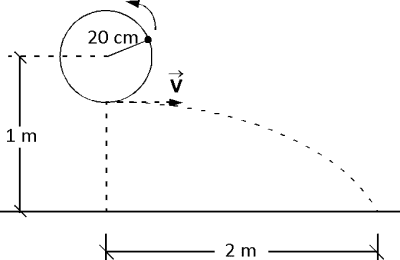
Un cuerpo de 200 g de masa gira en un plano vertical atado a una cuerda tensa de 20 cm de longitud. El eje del plano de giro se ubica a una altura de un metro del suelo. Cuando el cuerpo pasa por su punto más bajo la cuerda se rompe y el cuerpo cae a una distancia horizontal de 2 m como se muestra en la figura. Calcule la tensión de la cuerda (en N) en el momento que se rompe. ( g=9,81 m/s²)
A) 3,31
B) 6,62
C) 13,25
D) 26,49
E) 52,98
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 26 :
En un recipiente con agua se encuentra flotando un cuerpo sólido uniforme con el 90% de su volumen dentro del agua. Al recipiente se le agrega lentamente aceite hasta que el cuerpo queda totalmente sumergido, quedando el 20% del cuerpo dentro del agua, calcule la densidad del aceite (en kg/m³).
A) 775
B) 825
C) 875
D) 925
E) 975
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 27 :
Calcule aproximadamente la cantidad de calor, en kJ, que se desprende cuando 100 g de vapor de agua a 150 ºC se enfrían hasta convertirlo en 100 g de hielo a 0 ºC.
Calor específico de vapor de agua=2,01 kJ/kgK
Calor latente de vaporización del agua=2257 kJ/kg
Calor específico del agua líquida=4,18 kJ/kgK
Calor latente de fusión del agua=333,5 kJ/kg
A) 305
B) 311
C) 327
D) 332
E) 353
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 28 :
La intensidad media de una onda electromagnética es de 8 mW/m². Si la inducción magnética máxima de la onda aumenta en 25%, calcule, en mW/m², la nueva intensidad media.
A) 25
B) 27,5
C) 10
D) 15,5
E) 12,5
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 29 :
Un condensador almacena 5 nJ de energía cuando se le aplica una diferencia de potencial V. Si se conectan en serie 5 condensadores idénticos al anterior y se les aplica en los extremos la misma diferencia de potencial V. Calcule (en nJ) la energía total que se almacena en el circuito.
A) 1
B) 2
C) 3
D) 4
E) 5
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 30 :
En la figura se muestra la trayectoria que sigue un rayo de luz al pasar por los medios con índices de refracción n₁, n₂ y n₃. Determine el índice n₃ si n₁= 2,0.
A) 1,2
B) 1,8
C) 1,6
D) 0,83
E) 2,0
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 31 :
La intensidad de corriente eléctrica que circula por un alambre varía con el tiempo en la forma mostrada en la figura transportando una carga Q entre t=1 s y t=9 s. Calcule la intensidad de corriente eléctrica constante, en A, que transportaría la misma carga Q en el mismo intervalo de tiempo (entre 1 s y 9 s).
A) 1,5
B) 2,0
C) 2,5
D) 3,0
E) 3,5
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 32 :
Un protón tiene una energía cinética E y sigue una trayectoria circular en un campo magnético de magnitud B. Encuentre el radio de la trayectoria.
m: masa del protón ;
q: carga eléctrica del protón.
Rpta. : "D"
PREGUNTA 33 :
La densidad volumétrica de un planeta es 10% menos que la de la Tierra. Encuentre, aproximadamente, cuánto debe ser el radio del planeta, para que la aceleración de la gravedad en su superficie sea la misma que la de la Tierra. El radio de la Tierra es R.
A) 4,44R
B) 2,22R
C) 1,11R
D) 3,33R
E) 5,55R
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 34 :
La figura muestra un cuadrado ABCD de lado 1 u. Si las curvas son arcos de circunferencia con centros en B y D, exprese el vector →c en términos de →a y →b
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 35 :
Un cuerpo se lanza hacia arriba desde una altura de 20 m y alcanza una altura máxima (desde el suelo) de 30 m en un tiempo t. Si t' es el tiempo que demora el cuerpo en caer al suelo desde la altura máxima, calcule t'/t. ( g= 9,81 m/s²).
A) 1
B) √2
C) √3
D) 2
E) √5
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 36 :
La hélice de un ventilador gira a 960 RPM. Después de desconectarlo, desacelera uniformemente demorando 16 s hasta detenerse. Calcule el número de vueltas que realiza la hélice en la desaceleración.
A) 32
B) 64
C) 128
D) 256
E) 512
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 37 :
En el dibujo, el sistema sube con una aceleración de 0,19 m/s². Calcule la tensión (en N) en la cuerda que une los bloques A y B.
(mA= 400 g; mB= 300 g, mC= 200 g ; g= 9,81 m/s²)
A) 1
B) 2
C) 3
D) 4
E) 5
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 38 :
En la figura, el bloque pesa 90 N y es sometido a la acción de las fuerzas de módulos F1= 50 N y F2= 40 N. Calcule el trabajo (en J) que realiza F2 para un recorrido d, si se sabe que F1 realiza un trabajo de 400 J. ( g= 9,81 m/s²).
A) – 300
B) – 200
C) – 100
D) 100
E) 200
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 39 :
Una esfera de 200 cm³ de volumen que tiene una densidad igual a 0,8 g/cm³, está sumergida en un tanque lleno de agua. Si la esfera se suelta del fondo del tanque, calcule aproximadamente el tiempo (en s) que demora en elevarse 5 m dentro del agua. No considere las fuerzas de fricción. (g = 9,81 m/s²).
A) 2,02
B) 3,02
C) 4,02
D) 5,02
E) 6,02
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 40 :
Se calienta agua usando una cocina eléctrica de potencia P. En 10 minutos la temperatura del agua aumenta de 10° C a 100° C. Si la cocina sigue suministrando la misma potencia P, calcule aproximadamente el tiempo (en minutos) que se necesita para evaporar toda el agua. El proceso se realiza a presión normal.
Capacidad calorífica del agua:
4,18 × 10³ J ·kg–1 °C−¹
Calor latente de evaporación del agua:
2,257 × 10³ J ·kg−¹
A) 10
B) 30
C) 50
D) 60
E) 70
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 41 :
En un ciclo de Carnot de un gas ideal ( γ=5/3) , se tiene que durante la expansión isotérmica el volumen se duplica y en la expansión adiabática el volumen aumenta en un 25%. Calcule la relación entre la máxima y mínima temperatura en este ciclo
A) (1/4)2/3
B) (3/4)2/3
C) (5/4)2/3
D) (7/4)2/3
E) (9/4)2/3
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 42 :
Un condensador plano se carga en una batería de 6 V, luego se le desconecta. Después se disminuye la distancia de las placas de dicho condensador a la mitad. Calcule la diferencia de potencial (en V) entre las placas en este caso.
A) 1
B) 2
C) 3
D) 4
E) 5
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 43 :
En el circuito mostrado la potencia total disipada es de 75 W, calcula la resistencia R (en Ω).
A) 1
B) 2
C) 3
D) 4
E) 5
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 44 :
Una placa de estaño de 6 mm de espesor y de 4 cm² de área de sección recta, tiene la misma rapidez de transferencia de calor de una placa de hierro de 10 mm de espesor y de 9 cm² de área de sección recta. Calcule aproximadamente, en °C, la diferencia de las temperaturas exteriores de la placa de hierro, si para el estaño vale 5°C.
Las conductividades térmicas son 64 Wm−¹K−¹ y 80,2 Wm−¹K−¹ para el estaño y el hierro, respectivamente.
A) 3,96
B) 5,96
C) 4,96
D) 1,96
E) 2,96
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 45 :
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 46 :
Se tiene una porción de un cascarón esférico delgado que puede usarse como un espejo cóncavo o convexo. Se coloca un objeto a 100 cm de la parte cóncava formándose una imagen real a 75 cm del espejo. Sin mover al objeto se da vuelta al espejo de tal manera que la parte convexa mire al objeto y se mueve el espejo acercándolo o alejándolo del objeto hasta que se forme una imagen a 35 cm detrás del espejo. Calcule aproximadamente la distancia (en cm) que se desplazó el cascarón esférico.
A) 37,5
B) 70,3
C) 90,9
D) 123,4
E) 135,1
RESOLUCIÓN :
Rpta. : "C"