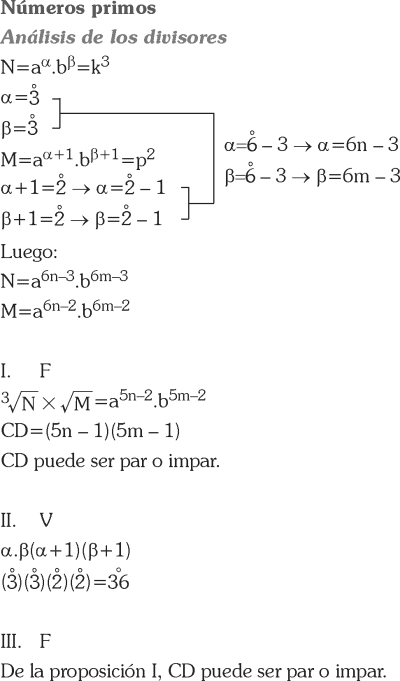ARITMÉTICA UNI PREGUNTAS RESUELTAS DE EXAMEN ADMISIÓN UNIVERSIDAD

PREGUNTA 1 : 

La suma de las cifras de los cuatro últimos dígitos de 

A) 11 

B) 13 

C) 16 

D) 17 

E) 19 

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 2 :

Las edades de Verónica y Sandra están en la relación de nueve a cinco. Si la suma de sus edades es 56, entonces ¿dentro de cuántos años Sandra tendrá la edad actual de Verónica? 

A) 20 

B) 18 

C) 16 

D) 12 

E) 8 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 3 : 

Indique la alternativa correcta después de determinar si la proposición es verdadera (V) o falsa (F), según el orden dado: 

I. Entre dos números racionales existe al menos un número irracional. 

II. El número 𝛑 se puede expresar exactamente como un número racional r = 22/ 7 . 

III. La suma de dos números irracionales es un número irracional. 

A) VVV 

B) VVF 

C) VFF 

D) FVF 

E) FFF 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 4 :

Cerca a una determinada isla se encuentran cuatro faros, el primero de ellos se enciende cada 12 segundos, el segundo cada 18 segundos, el tercero cada 48 segundos y el cuarto cada minuto. Si a las 20:45 coinciden, ¿a qué hora volverán a coincidir? 

A) 20:59 

B) 20:55 

C) 20:54 

D) 20:57 

E) 20:56 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 5 : 

Un termómetro fallado indica 5 °C para el hielo y marca 125 °C para el vapor de agua hirviendo. Entonces la temperatura real en grados Celsius cuando dicho termómetro marca 38 °C es 

A) 27,4 

B) 27,8 

C) 27,6 

D) 27,5 

E) 27,7 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 6 : 

Se elige aleatoriamente un número entero de cinco cifras. Calcule la probabilidad que dicho número sea par y la suma de sus cifras sea 42. 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 7 : 

mujeres; además, son c aeromozas y a pilotos. Si el número de personas está comprendido entre 150 y 300. 

Determine cuántos hombres más que mujeres hay en total. 

A) 179 

B) 178 

C) 182 

D) 181 

E) 180 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 8 : 

Se dispone de tres recipientes cúbicos cuyos lados de longitud L1, L2, L3 cumplen con la siguiente condición: 

Se pretende distribuir 434 litros de agua entre los tres recipientes de modo que alcancen el mismo nivel o altura. Determine los litros de agua que recibe el recipiente de longitud L2. 

A) 112 

B) 120 

C) 124 

D) 136 

E) 146 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 9 :

Las notas de un determinado examen son 

7, 8, 9, 9, 10, 10, 12, 13, 14, 14, 15, 17, 18 y 19 

Determine el valor de la media de las notas dadas. 

A) 12.7 

B) 12.4 

C) 12.6 

D) 12.5 

E) 12.8 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 10 : 

Considere la progresión aritmética 

donde la suma de los tres primeros términos es mayor que 170. Si n es el menor posible, calcule la suma de los primeros 12 términos de esta progresión. 

A) 1150 

B) 1330 

C) 1340 

D) 1350 

E) 1650 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 11 : 

Consideremos el número 

Determine el residuo de dividir p entre ocho. 

A) 3 

B) 6 

C) 7 

D) 5 

E) 4 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 12 : 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 13 : 

Considere a 

Determine el valor de a(50) – 0,01. 

A) 0,96 

B) 0,98 

C) 0,95 

D) 0,99 

E) 0,97 

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 14 : 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 15 :

Un obrero desea terminar una obra en veinte días trabajando solo, pero si contrata a dos amigos, terminarían la obra en doce días. ¿En cuántos días culminarían la obra solo él y cinco amigos? Suponga que trabajan con el mismo rendimiento. 

A) 7 

B) 9 

C) 6 

D) 10 

E) 8 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 16 : 

Sea la fracción a/3 (a y 3 primos entre sí), con a > 0. 

Al numerador le agregamos el número A∈N y al denominador 2A, se obtiene una fracción equivalente que es la mitad de la fracción original, entonces la suma de todos los valores posibles de a es: 

A) 4 

B) 8 

C) 9 

D) 12 

E) 15 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 17 : 

Indique la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F). 

I. Población es el conjunto del cual se van a estudiar los datos para eliminar los extraños. 

II. Variable es una característica de la población que interesa al estadístico y que puede tomar diferentes valores. 

III. Muestra es un subconjunto de la población, la cual es representativa que permita hacer deducciones de ella respecto al total de la población. 

A) VFF 

B) FFF 

C) FVV 

D) VVV 

E) VFV 

RESOLUCIÓN :

I. FALSA 

En estadística, población es el conjunto de todos los elementos de interés en un determinado estudio. 

En la proposición planteada, la primera parte es coherente con la definición de población, pero no la última parte que menciona “para eliminar los extraños”. 

II. VERDADERA 

En estadística, variable es una característica que interesa observar o medir y que puede asumir al menos dos valores diferentes. 

En la proposición, es correcta la definición que dan de variable. 

III. VERDADERA 

En estadística, muestra es un subconjunto de la población. 

En la proposición es correcta la definición que dan de muestra.

Rpta. : "C

PREGUNTA 18 :  

Sea r el residuo de dividir 

Determine cuáles de las siguientes proposiciones son verdaderas. 

I. r=6, si n es par. 

II. r=6, si n es impar. 

III. r=2, si n es impar. 

A) solo I 

B) solo II 

C) solo III 

D) I y II 

E) I y III 

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 19 : 

Se funden 900 gramos de una aleación con 100 gramos de oro puro y se observa que la ley se incrementa en 0,04 con respecto a la ley primitiva. Entonces la ley de la aleación inicial es 

A) 0,62 

B) 0,64 

C) 0,60 

D) 0,68 

E) 0,66

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 20 : 

El perímetro de un triángulo es 50 m y sobre cada lado del triángulo se forma un cuadrado cuyo lado coincida con el lado del triángulo. Como resultado, la suma de las áreas de los cuadrados formados es 900 m² y el lado del primer cuadrado es al del segundo como, el lado del tercero es a la mitad del primero. La relación del mayor y el menor de los lodos del triángulo es de (Considere que los lados del triángulo son números naturales) 

A) 2 a 1 

B) 5 a 2 

C) 3 a 1 

D) 5 a 1 

E) 11 a 2 

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 21 : 

Marta invierte 16 000 soles al 20% durante cinco años. Si el interés se acumula continuamente, entonces el monto acumulado al final (en soles), es aproximadamente 

(Use el valor e =2,71828) 

A) 43 495,88 

B) 43 493,68 

C) 43 491,58 

D) 43 492,48 

E) 43 490,78 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 22 : 

Las magnitudes X e Y son tales que (Y – 2) y (X²+ 1) son inversamente proporcionales. Se sabe que cuando X= 2, se tiene que Y= 3. Determine la ecuación que relaciona X e Y 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 23 :

Determina el tiempo de vencimiento común de tres letras de cambio de valores nominales iguales cuyos tiempos de vencimiento son: 24 días, 72 días y 5 meses. 

A) 86 

B) 82 

C) 85 

D) 83 

E) 84 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 24 : 

Cualquier tipo de café crudo pierde el 20% de su peso al tostarlo. Se ha comprado dos tipos de café crudo cuyos precios por kilogramo son 10 y 15 soles respectivamente. 

Si todo el café tostado se vendiera a 15 soles el kilogramo no se ganaría ni se perdería, pero se vendió todo el café tostado en S/3240 ganando el 20% del costo. Halle la suma de los pesos iniciales y dé como respuesta la diferencia de la mayor cifra con la menor cifra del resultado. 

A) 6 

B) 5 

C) 4 

D) 3 

E) 2 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 25 :

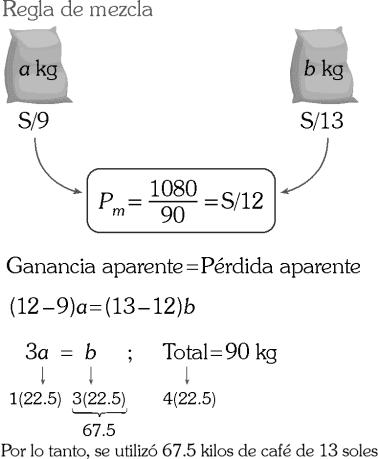
Julia compró 90 kilos de café a 1080 soles. Ella sabe que dicho café es la mezcla de dos tipos diferentes, cuyos precios “por kilo” son 9 y 13 soles, respectivamente. 

Entonces, la cantidad de kilos de café de 13 soles que usó es 

A) 69.0 

B) 69.5 

C) 67.5 

D) 68.5 

E) 68.0 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 26 : 

El número de hijos por familia en una determinada ciudad es una variable aleatoria H, cuya función de probabilidad es

 f(x)=P[H=x]=Kx/5 

x = 1; 2; 3; 4; 5 

¿Cuál es la probabilidad de que una familia tenga 3 hijos dado que tiene al menos dos hijos? 

A) 0,200 

B) 0,333 

C) 0,214 

D) 0,267 

E) 0,357 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 27 :

En una urna se tiene cuatro fichas numeradas: 1, 2, 3, 4, y de ellas se extraen dos fichas sin reposición. Si X es la variable aleatoria que representa la suma de los cuadrados de los dos números obtenidos, determine la esperanza de dicha variable. 

A) 12 

B) 15 

C) 21 

D) 18 

E) 24 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 28 : 

Se tienen 496 números naturales consecutivos. Al dividir el número anterior al mayor entre el número menor de la lista de números, se obtiene como residuo 49 y como cociente un número natural diferente a 6. Indique la cifra de las centenas del número que se obtiene al multiplicar el trigésimo segundo número y el centésimo tercer número. 

A) 0 

B) 1 

C) 2 

D) 3 

E) 4 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 29 : 

Halle un número de la forma

tal que sea múltiplo de44 

Dar como respuesta el residuo que se obtiene al dividir dicho número entre 5. 

A) 0 

B) 1 

C) 2 

D) 3 

E) 4 

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 30 :

Determine la suma de las cifras del menor número

de tal manera que sea un cubo perfecto. 

A) 26 

B) 29 

C) 27 

D) 30 

E) 28 

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 31 : 

Indique la secuencia correcta después de determinar si la proposición es verdadera (V) o Falsa (F). 

I. El producto de un número irracional por otro irracional es siempre irracional. 

II. La suma de dos números irracionales siempre es un número irracional. 

III. Entre dos números racionales diferentes siempre existe otro número racional. 

A) VVV 

B) VFV 

C) VFF 

D) FFF 

E) FFV 

RESOLUCIÓN :

Tema: Conjunto de los racionales

I) Falso 

Veamos un contraejemplo (√3 −1) (√3 +1)=3 −1 

irracional×irracional racional 

Por lo tanto, el producto de dos números irracionales puede resultar un número racional. 

II) Falso 

Veamos un contraejemplo (1−√2)+(1−√2)= 2 

irracional+irracional racional 

Por lo tanto, la suma de dos números irracionales puede resultar un número racional. 

III) Verdadero 

Se sabe que el conjunto de los números racionales es un conjunto denso; es decir, entre dos racionales cualesquiera hay infinitos racionales. 

Por lo tanto, entre dos racionales diferentes siempre existe otro números racionales. 

Rpta. : "E"

PREGUNTA 32 : 

A) 4 

B) 0 

C) 2 

D) 1 

E) 3 

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 33 : 

Sean A, B y D subconjuntos de los números reales y definimos el operador * mediante 

A * B= (A ∩ B)^C 

Indique el valor de verdad de las siguientes proposiciones. 

I. (A * B) * D=A *(B * D) 

II. (A * B) * A = A * (B * A) 

III. A * ∅ = ∅ 

Donde A^C indica el complemento de A. 

A) VFF 

B) FVV 

C) VVV 

D) FFF 

E) FVF 

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 34 :

Si A⊂ B simplifique: 

[A ∩ (A ∪ B^c)] ∩ [B ∪ (A ∪ B^c)^c] 

A) A∪B^c 

B) A^c∪B 

C) A 

D) B 

E) A/B 

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 35 : 

Seleccione le gráfica que mejor represente las premisas: 

“Todos los que compiten son valientes. 

Ningún simple compite” 

C: Compiten , V: Valientes , S: Simples 

RESOLUCIÓN :

Rpta. : "C"