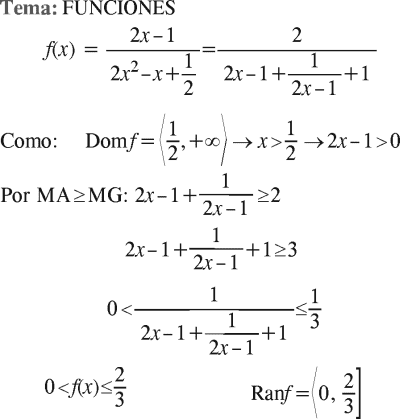ÁLGEBRA UNI PREGUNTAS RESUELTAS DE EXAMEN ADMISIÓN UNIVERSIDAD
PREGUNTA 1 :
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 2 :
Determine el conjunto solución de la ecuación
Log(5 – x)(35 – x³) = 3.
A) ∅
B) {2; 3; 4; 6}
C) {3; 4}
D) {2; 3}
E) {2; 3; 4}
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 3 :
Halle el conjunto solución de la siguiente inecuación
A) 〈–7, – 3〉 ∪ {0}
B) 〈– ∞, – 5〉 ∪ 〈– 3, 0]
C) 〈– 5, – 2〉 ∪ {0}
D) 〈– 5, – 3〉 ∪ {0}
E) 〈– 5, –1〉 ∪ {0}
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 4 :
Calcule el valor de 16a²+ 5
A) 30
B) 10
C) 25
D) 15
E) 20
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 5 :
Algunos científicos afirman que el promedio de la temperatura de la superficie de la Tierra está subiendo constantemente.
El promedio de la temperatura de la superficie de la Tierra lo han modelado como sigue:
T=0,02t +15,0
donde T es la temperatura en °C y t en años desde 1950.
Por lo tanto, se puede pronosticar que la temperatura promedio en °C de la superficie de !a Tierra en el año 2050 será
A) 15
B) 14
C) 18
D) 16
E) 17
RESOLUCIÓN :
FUNCIONES
Desde 1950 hasta 2050, han transcurrido 100 años.
⇒ T = (0,02(100) + 15,0) °C
⇒ T = 17 °C
Rpta. : "E"
PREGUNTA 6 :
Sea :
p(x) = x⁴ + 2x³ + 3x² + 5
q(x) = x² + 5x – 4.
Sea r(x) el resto que se obtiene al hacer la división de p(x) entre q(x).
Halle r(1).
A) – 35
B) – 33
C) – 31
D) – 29
E) – 27
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 7 :
Una empresa de artefactos electrodomésticos determina que si produce X hornos tostadores por mes, su costo Y de producción está dado por la ecuación como sigue:
Y=6X+3000
donde Y se mide en dólares.
Si el costo de producción fuese de 3600 dólares, entonces el número de tostadores es
A) 80
B) 110
C) 100
D) 70
E) 90
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 8 :
Sean las ecuaciones
y=x² – 3x+4
y=mx+3
Determine los valores reales de m para que nunca se intersequen.
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 9 :
Sea :
F(x) =x² + 1
(G o F)(x) =x⁴ – 4x²+ 4
Halle y ∈ R tal que G(y) =0
A) 1
B) 4
C) 3
D) 2
E) 5
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 10 :
Del sistema de ecuaciones
x² – x – a =0
x² + x + b =0
Sea r una raíz común y sabiendo que a + b = 3, entonces el módulo de la suma de las otras raíces es
A) 9
B) 7
C) 3
D) 5
E) 0
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 11 :
Determine los puntos de intersección de la gráfica de la función definida por
f (x) =│x − 2│+ x² con la recta 3x – 2y= – 11.
A) ( – 1; 2), (3; 9)
B) (1; – 4), (3; 10)
C) (–1; 4), (3; 10)
D) ( – 1; 1), (4; 9)
E) (1; – 4), (3; 12)
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 12 :
El valor de la serie es igual a
A) 0,26
B) 0,30
C) 0,25
D) 0,28
E) 0,27
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 13 :
Al efectuar la división
el término independiente del cociente que resulta es
A) – 2n
B) – n
C) 0
D) n
E) 2n
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 14 :
Halle el módulo de z, donde
A) 5√2
B) 6√2
C) 3√2
D) 7√2
E) 4√2
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 15 :
Si E=〈– ∞; 2] es el conjunto solución de la inecuación |x – a| ≤ |x – b| , 0<a<b, entonces el menor valor de (a+b)² es:
A) 8
B) 10
C) 12
D) 14
E) 16
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 16 :
g(x) =Ln(x), indique la secuencia correcta después de determinar si la proposición es verdadera (V) o falsa (F).
I. Para todo x>0 se tiene
Log₄(2x+1) >Log₂(x+1).
II. La función logaritmo es creciente.
III. La función exponencial es creciente.
A) VFF
B) VFV
C) VVV
D) FFF
E) FVF
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 17 :
Sean a; b; c ∈ R tales que 0<a<b <c y x1<x2. Siendo (x1; y1) y (x2; y2) soluciones del sistema de ecuaciones
y=ax²+bx+c
y=cx²+bx+a
entonces podemos afirmar que
A) x1, x2, y1, y2 >0
B) x1, x2 <0; y1, y2 >0
C) x1, x2 >0; y1, y2<0
D) x1<0; x2, y1, y2 >0
E) x1 >0; y1, y2<0
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 18 :
Sea f: [–1; 1] → R una función decreciente y h la función definida por h(x) = f(2 – x).
I. Dom(h) = [–1; 1]
II. h es una función creciente.
III. – h es una función creciente.
Indique cuáles de las siguientes proposiciones son verdaderas.
A) solo I
B) I y II
C) solo II
D) solo III
E) I y III
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 19 :
Dado el conjunto S={x∈ℝ / 0<Log|x –1| < 1}
Determine S ∩ ([0; 2] ∪ [12; 20]).
A) ∅
B) 〈1; 2〉
C) [15; 20]
D) [12; 15]
E) [12; 20]
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 20 :
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 21 :
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 22 :
Dada la siguiente sucesión (donde [x] máximo entero de x).
xn= [ n(−1 )ⁿ/ eⁿ]
¿Cuál de las siguientes afirmaciones es verdadera con respecto a xn?
A) Es constante a partir de cierto n.
B) Es decreciente.
C) No es convergente.
D) Es creciente.
E) Converge a 0.
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 23 :
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 24 :
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 25 :
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 26 :
Calcule:
Dar como respuesta la primera cifra decimal.
A) 0
B) 1
C) 2
D) 3
E) 4
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 27 :
Definimos el conjunto
Considere las siguientes proposiciones:
I. La suma de los elementos del conjunto A es 7.
II. Card(A)=2
III. 2√2−2 ∈A
Determine de las proposiciones dadas cuáles son verdaderas.
A) solo I
B) solo II
C) solo III
D) I y II
E) I y III
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 28 :
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 29 :
Halle el polinomio p(x) de coeficientes racionales de menor grado con raíces 1 y 1+√2, y que además cumpla p(0) = 1.
Dé como respuesta la suma de los coeficientes del polinomio.
A) –2
B) –1
C) 0
D) 1
E) 3
RESOLUCIÓN :
Tema: Polinomios
Del dato se tiene que 1 es una raíz.
Entonces
P(1) =0
Por propiedad
P(1) = suma de coeficientes
→ P(1) =0= suma de coeficientes
Rpta. : "C"
PREGUNTA 30 :
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 31 :
RESOLUCIÓN :
Rpta. : "C"