TRIGONOMETRÍA UNI PREGUNTAS RESUELTAS DE EXAMEN ADMISIÓN UNIVERSIDAD
PREGUNTA 1 :
Sean :
α=4𝛑/15
β= 40°
γ=60 grados centesimales
y las expresiones
M=α+β
N=(2α+β+γ)/3
P=4β – γ
Q=3α – β
R=α/2 + 2β + γ/2
entonces la expresión de mayor valor es:
A) Q
B) P
C) R
D) N
E) M
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 2 :
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 3 :
Dos estudiantes de 2 metros de altura alineados sobre una misma línea recta y separados a una distancia de 1 metro, observan con ángulos de elevación α y β (α> β), respectivamente, un poste de 4 metros de altura.
Si tanα + tanβ = 3/2
Entonces la distancia en metros del estudiante que se encuentra más cerca del poste es
A) (3 + √73)/6
B) (4 + √73)/6
C) (5 + √73)/6
D) (2 + √73)/6
E) (6 + √73)/6
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 4 :
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 5 :
Si tanx + cotx= 3, entonces el valor de
M= (tan⁴x – sec⁴x)(csc⁴x – cot⁴x) es
A) –16
B) –20
C) –18
D) –17
E) –19
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 6 :
Si
el valor de
M= 3(sec²x+ csc²x) es
A) 3 [(1 – 2m)/(m – 2)]
B) [(1 – 2m)/(m – 2)]
C) 4 [(1 – 2m)/(m – 2)]
D) 5 [(1 – 2m)/(m – 2)]
E) 2 [(1 – 2m)/(m – 2)]
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 7 :
Un marino que observa el horizonte desde un faro de altura h, lo hace con un ángulo de depresión θ. Calcule el radio R de la Tierra en función de h y θ.
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA8 :
En la figura adjunta
Si M y N trisecan al segmento AB, entonces el valor de
√13senα+ √5senθ es:
A) 3
B) 5
C) 1
D) 4
E) 2
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 9 :
En [ – 𝛑/2 ; 𝛑] , la suma de las raíces de la ecuación
2sen⁴x + sen²x −1= 0 es
A) 𝛑
B) 5𝛑/4
C) 3𝛑/4
D) 𝛑/2
E) 𝛑/4
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 10 :
La suma de los valores del conjunto de solución de la siguiente ecuación
arccosx – arcsenx= arcsen(2 – 3x) es
A) 1,3
B) 1
C) 1,4
D) 1,5
E) 1,2
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 11 :
A) 2cos(θ) – sen(θ)
B) cos(θ) – sen(θ)
C) 2sen(θ) – cos(θ)
D) sen(θ) + cos(θ)
E) sen(θ) – cos(θ)
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 12 :
El dominio de la función f definida por
A) [1; 2]
B) [1; 1,4]
C) [1; 1,8]
D) [1; 2,2]
E) [1; 1,6]
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 13 :
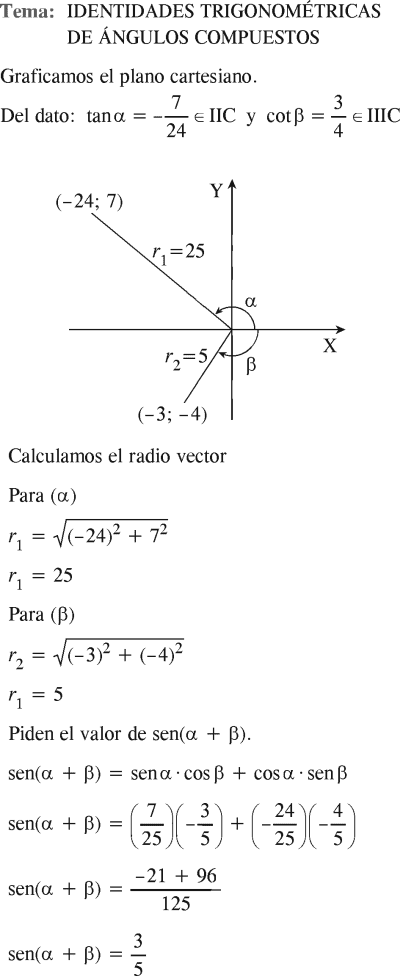
Sea α un ángulo en el II cuadrante con tan(α)=−7/24 y β un ángulo en el III cuadrante con cot(β)=3/4 Determine el valor de sen(α+β).
A) − 107/125
B) − 3/5
C) 17/125
D) 3/5
E) 107/125
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 14 :
Al resolver cos2x ≤ √3/2 ; ∀∈[0; π] se tiene como solución a
A) [ 𝛑/12 ; 9𝛑/12 ]
B) [ 𝛑/12 ; 7𝛑/12 ]
C) [ 𝛑/12 ; 11𝛑/12 ]
D) [ 𝛑/12 ; 10𝛑/12 ]
E) [ 𝛑/12 ; 8𝛑/12 ]
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 15 :
Dada la ecuación general de la cónica : Ax²+By²+Cx+Dy+F=0 con A, B, C, D, F constantes arbitrarias, se tiene que:
I. Si A=B ≠ 0, entonces siempre tenemos la ecuación de una circunferencia.
II. Si B=0 y A ≠ 0, entonces siempre tenemos la ecuación de una parábola.
III. Si A.B<0 y D² – 4BF<0, entonces siempre tenemos la ecuación de una hipérbola.
Luego son verdaderas:
A) solo I
B) II y III
C) solo II
D) solo III
E) I y III
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 16 :
Una elipse con centro en el origen de coordenadas tiene como recta directriz :
x+2y – 6= 0
Si la longitud del eje mayor es el triple del eje menor, entonces la distancia entre los focos es
A) 32√5/13
B) 32√5/15
C) 32√5/14
D) 32√5/11
E) 32√5/12
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 17 :
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 18 :
Si S y C son los números de las medidas en grados sexagesimales y en grados centesimales, respectivamente, para un mismo ángulo, que cumple
125^(S –1)=25^C
Determine la medida de dicho ángulo en radianes.
A) 3𝛑/138
B) 3𝛑/139
C) 3𝛑/141
D) 3𝛑/137
E) 3𝛑/140
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 19 :
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 20 :
En un triángulo ABC cuyo semiperímetro es p, el valor de
A) 1
B) 4
C) 2
D) 3
E) 0
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 21 :
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 22 :
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 23 :
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 24 :
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 25 :
Si la gráfica de y=Aarccos(Bx+C) +D es
determine el valor de E=A+B+C.
A) 3
B) 2/3
C) 4/3
D) 4
E) 14/3
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 26 :
Obtenga el conjunto solución del siguiente sistema de ecuaciones:
y = 1 – cosx
1 = 4ycosx
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 27 :
Determine el menor periodo positivo de la función definida por
A) π/2
B) π
C) 3π/2
D) 2π
E) 4π
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 28 :
El menor ángulo de un paralelogramo mide a y sus diagonales miden 2m y 2n. Calcule su área. (m > n)
A) (m² – n²)tan(α)
B)(m² – n²)cot(α)
C) (m² – n²)sec(α)
D)(m² – n²)csc(α)
E)(m² – n²)sen(α)
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 29 :
La ecuación de una cónica en coordenadas polares es
Determine una ecuación cuadrática para sus puntos en coordenadas rectangulares
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 30 :
Sea
Halle la suma de valores del Rango(f ).
A) 8n+3
B) 8n
C) 8n+1
D) 8n+2
E) 8n – 1
RESOLUCIÓN :
Rpta. : "D"