ÁLGEBRA SAN MARCOS PRUEBA DECO RESUELTA DE ADMISIÓN UNIVERSIDAD
PREGUNTA 1:
El domingo pasado, un museo recibió cierto número de visitantes. Hasta el mediodía lo habían visitado 42 personas y en la tarde asistió el resto, que era más de las tres quintas partes del número total de visitantes. Después del mediodía hasta las 4:00 p. m., 31 personas visitaron el museo, y los que lo visitaron después de las 4:00 p. m. fueron menos de 34 personas. ¿Cuántas personas visitaron el museo después del mediodía?
A) 60
B) 65
C) 68
D) 66
E) 64
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 2 :
Dos números consecutivos no negativos tienen la siguiente propiedad: el cuadrado de su producto excede en 90 al doble del cubo del menor de ellos. ¿Cuánto suman dichos números?
A) 7
B) 11
C) 9
D) 13
E) 6
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 3 :
Dado el conjunto
A) 4
B) 0
C) 3
D) 1
E) 5
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 4 :
Un comerciante compró cierta cantidad entera de kg de arroz, luego vendió 38 kg y le quedó más de la mitad de lo que había comprado. Al día siguiente, logró vender 15 kg y le quedó, finalmente, menos de 25 kg. ¿Cuántos kg de arroz compró el comerciante inicialmente?
A) 76
B) 81
C) 80
D) 78
E) 77
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 5 :
Con respecto a las raíces del polinomio p(x)=x³ – 7x+m ; m∈ℝ, se sabe que una raíz es positiva e igual al doble de otra. Halle la suma de los cubos de todas las raíces de este polinomio.
A) – 24
B) – 18
C) – 21
D) – 9
E) –4
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 6:
La administración de un hotel adquirió un total de 200 unidades entre almohadas, mantas y sábanas, por lo que gastó un total de 7500 soles. El precio de una almohada fue 16 soles; el de una manta, 50 soles y el de una sábana, 80 soles. Además, el número de almohadas compradas fue igual al número de mantas sumado con el número de sábanas. ¿Cuántas unidades más de almohadas que de sábanas compró?
A) 70
B) 30
C) 100
D) 40
E) 64
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 7 :
Con un rollo completo de alambre es posible cercar un terreno de forma cuadrada. Si con la misma cantidad de alambre se puede cercar un terreno de forma rectangular, con un lado 6 metros mayor que el otro lado y de área mayor o igual a 40 m², ¿cuántos metros puede medir, como mínimo, el perímetro del terreno de forma cuadrada?
A) 24
B) 32
C) 20
D) 28
E) 22
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 8 :
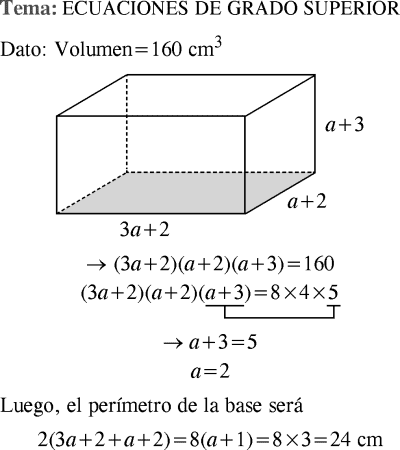
Se tiene un sólido compacto, con forma de un paralelepípedo rectangular recto, cuyas dimensiones de su base son (a + 2) cm y (3a + 2) cm. Si su altura mide (a + 3) cm y su volumen es 160 cm³, determine el perímetro de su base en centímetros.
A) 48
B) 32
C) 16
D) 24
E) 28
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 9:
Jaime tiene una pequeña empresa dedicada a fabricar polos. Su ingreso semanal en soles está determinado por la función I(x)=ax²+bx, donde x representa el número de polos vendidos en una semana. Si se venden 120 polos en una semana, el ingreso es de S/.5760; además, la venta de 300 polos semanales genera el ingreso máximo. Halle el ingreso que se obtiene en una semana en la que se venden 200 polos.
A) S/.6000
B) S/.7800
C) S/.8200
D) S/.8500
E) S/.8000
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 10:
Un móvil se desplaza a velocidad constante desde el punto M hasta el punto N, siguiendo el recorrido dado por la gráfica de la función f(x)=5 –|x – 4|, x ∈ [0;9]. Si las coordenadas de M y N son (0; f(0)) y (9; f(9)), halle la distancia recorrida por el móvil sabiendo que x se mide en kilómetros.
A) 12√2 km
B) 10√2 km
C) 8√2km
D) 12√2km
E) 9√2km
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 11 :
La población de cierto tipo de bacterias se obtiene según el modelo P(t)=k[At] , t ∈ [0, 5], donde P(t) representa el número de bacterias después de t horas, donde {k ; A}⊂ℝ+. Si la población inicial era de 100 bacterias (t=0) y, dos horas después, había 400 bacterias, ¿cuántas bacterias habrá después de dos horas más?
A) 2800
B) 800
C) 1600
D) 2000
E) 2400
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 12 :
Se coloca 4 kilogramos de una sustancia en un recipiente con agua y, cada minuto, se diluye el 19% de la cantidad de esta sustancia. Si la cantidad de sustancia no diluida, al cabo de t minutos, está dada por la función Q(t), en kilogramos, halle una expresión equivalente para Q(t/2)
A) 4×(0,19)t/2
B) 2×(0,81)t/2
C) 4×(0,81)t/2
D) 4×(0,9)t
E) 4×(0,6)t
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 13 :
Un comerciante textil alquila un total de 19 máquinas, entre remalladoras, bordadoras y de coser, a 80 ; 50 y 60 dólares, respectivamente, y obtiene un total de 1240 dólares semanales. Si aumentara en 20 dólares el alquiler de cada remalladora, en 10 dólares el alquiler de cada máquina de coser y disminuyera en 10 dólares el alquiler de cada bordadora, obtendría un total de 1420 dólares a la semana. ¿Cuántas máquinas bordadoras alquila semanalmente?
A) 7
B) 4
C) 6
D) 5
E) 2
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 14 :
Un escolar gastó cierta suma de dinero para comprar un maletín, un lapicero y un libro. Si el costo de los útiles fuese 1/10 ; 1/4 y 1/5 de los precios originales, respectivamente, el gasto sería 8 soles; en tanto que si el costo fuese 1/4 ; 1/8 y 1/6 de los precios originales respectivamente, el gasto sería 12 soles. ¿Cuántos soles gastó dicho escolar?
A) 48
B) 50
C) 65
D) 60
E) 56
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 15:
Un comerciante vende tres variedades de quinua: roja, negra y amarilla. Los precios de cada kilogramo de estas variedades de quinua son S/.18, S/.20 y S/.10 respectivamente. Al finalizar el día, vendió un total de 40 kg de quinua y el importe por todo lo vendido fue de S/.576. Si el número de kilogramos vendidos de quinua roja menos los de quinua negra es la quinta parte del número de kilogramos vendidos de quinua amarilla, ¿cuántos kilogramos se vendió de la quinua que tuvo mayor demanda?
A) 20
B) 24
C) 18
D) 22
E) 26
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 16 :
Si M es el menor número entero que satisface la desigualdad −x² +2x − 2,5 <M, para todo x∈ℝ , halle el valor de M² – 6M+ 9.
A) 1
B) 9
C) 4
D) 16
E) 2
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 17 :
En un estudio oceanográfico, se observó que la temperatura del agua, en grados Fahrenheit, es dada por
T(x) = log(x + 2) + log(2 – x)
donde x es un parámetro relacionado con la salinidad del agua. Las condiciones de supervivencia de cierta especie exigen que esta temperatura sea positiva. Determine los valores que puede tomar el parámetro x para garantizar la supervivencia de esta especie. Dé como respuesta la suma de los valores enteros que puede tomar este parámetro.
A) – 1
B) 1
C) 0
D) 2
E) 3
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 18 :
Una empresa, que tiene un costo fijo mensual de 2100 soles, fabrica para smartphones. El precio de venta de cada funda es de 40 soles y el costo para producirla es el 55% del precio de venta. Si logran vender toda la producción mensual de fundas, ¿cuál es el número que deben producir y vender para que la utilidad mensual sea 7980 soles?
A) 710
B) 620
C) 450
D) 560
E) 640
Rpta. : "D"
PREGUNTA 19 :
Una librería tiene disponible, en total, treinta lapiceros distribuidos en tres colores: rojo, negro y azul, donde al menos hay uno de cada color. Los precios por unidad son, respectivamente, 4 ; 3 y 2 soles. Jorge deberá pagar 110 soles por la compra de todos los lapiceros disponibles. ¿Cuántos lapiceros de color rojo comprará Jorge si debe adquirir la mayor cantidad de lapiceros azules?
A) 26
B) 25
C) 23
D) 22
E) 24
Rpta. : "E"