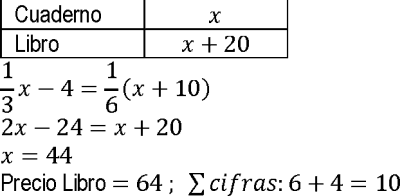ÁLGEBRA DE EXAMEN ADMISIÓN UNIVERSIDAD PRUEBA AUTO EVALUACIÓN CON CLAVES RESPUESTAS
PREGUNTA 1 :
Calcule la solución entera positiva de:
2x² + 3x = 44
A) 3
B) 4
C) 2
D) 8
E) 11
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 2:
En la sala de ventas, Bruno contó que al doble del número de autos más el triple de motocicletas es 280. Si la diferencia entre el número de llantas de autos y de motos es 240, ¿cuántos móviles hay en la tienda?
A) 120
B) 160
C) 180
D) 200
E) 360
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 3 :
Determine el valor numérico de
sabiendo que x = 2019
A) 2
B) 3
C) 9
D) 2019
E) 45
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 5:
Halle el valor de "x":
A) –2
B) –1
C) 1
D) 2
E) 3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 6:
Halle el valor de:
A) 14
B) 15
C) 17
D) 18
E) 20
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 7:
Sabiendo que: x.y > 0 , se cumple, x(19y−10x)=6y². Halle la razón x/y
A) 3/2; 2/5
B) 1/3; 1/5
C) 2/3; 1/2
D) 4/5: 2/3
E) 2/3; 2/5
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 8:
Jenny compró 8 plátanos y pagó con una moneda de 5 soles, pero no recuerda cuanto le dieron de vuelto. José compró una docena de los mismos plátanos, pero tuvo que volver a casa porque los S/. 6,50 que llevó no le alcanzaron. ¿Entre qué valores está el precio del plátano?
A) 〈0,541; 0,625〉
B) 0,201; 0,302
C) 〈0,303; 0,400〉
D) 〈0,401; 0,500〉
E) 〈0,630; 0,700〉
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 9:
El precio de un cuaderno es de S/ 20 menos que el precio de un libro. Si a la tercera parte del precio del cuaderno se le disminuye S/ 4, se obtiene la sexta parte del precio del libro. ¿Halle la suma de cifras del precio del libro?
A) 12
B) 9
C) 8
D) 10
E) 7
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 10:
En tres días una agencia bancaria recibió S/ 16 800. Halle el ingreso del tercer día sabiendo que cada día el banco recibió 1/4 de lo que recibió el día anterior.
A) S/ 800
B) S/ 900
C) S/ 700
D) S/ 1 000
E) S/ 1 200
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 11:
En un gallinero había cierto número de gallinas. Se duplicó el número y se vendieron 27, quedando menos de 54. Después se triplicó el número de gallinas que había al principio y se vendieron 78, quedando más de 39. ¿Cuántas gallinas había al principio?
A) 41
B) 42
C) 40
D) 38
E) 39
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 12:
Determine el conjunto solución de:
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 13 :
Forme la ecuación cuadrática de raíces 0 y 4.
A) x²+4x = 0
B) x² = 16
C) x² – 4x = 0
D) x² = 4
RESOLUCIÓN :
Aplicando la propiedad de la formación de una ecuación cuadrática a partir de sus raíces :
x² – (0+4)x+(0).(4)=0
⇒ x² – 4x=0
Rpta. : "C"
PREGUNTA 14 :
Cuatro operaciones 5 adultos y 8 niños acuerdan ir al cine. Si el precio de las entradas para adultos es el doble del precio de las entradas para niños, sabiendo que se pagó 270 soles, halle el precio de la entrada para un adulto.
A) 15 soles
B) 30 soles
C) 45 soles
D) 60 soles
RESOLUCIÓN :
De los datos:
Precio de las entradas al cine:
Adulto: 2x
Niño: x
Cantidad de personas:
Adultos: 5
Niños: 8
Entonces de acuerdo a lo pagado:
5(2x)+8(x)=270 x=15 (precio de entrada para niño)
∴ 2x=30 (precio de entrada para adulto)
Rpta. : "B"
PREGUNTA 15 :
Si x∈〈–3;0〉 , halle la variación de:
A) 〈–2/5;0〉
B) 〈1/2;5/2〉
C) 〈–5/2;1/2〉
D) 〈–2/5;1/2〉
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 16 :
A) 2y
B) √2y
C) 2√y
D) √y
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 17 :
Si la solución de la ecuación
es “m”, halle el valor de 6m+5.
A) 1
B) 2
C) 3
D) 4
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 18 :
Si – 3 < x < 5, halle el intervalo de variación de la expresión
A) 〈0;2/3〉
B) 〈–2/3;0〉
C) 〈2/3;3/2〉
D) 〈– 3;2/3〉
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 19 :
Siendo F una función lineal tal que (1;2) y (4;6) son coordenadas que pertenecen a la función F y G(x)=– 2x+3, calcule la suma de las pendientes de las funciones lineales F y G.
A) – 1/3
B) – 2/3
C) 1/5
D) 1/3
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 20 :
Si yo tuviera 27 años menos, el tiempo que pasaría despierto sería la quinta parte del que permanecería dormido si tuviera 27 años más. Si duerme 8 horas diarias, halle la edad que tenía hace 12 años.
A) 18
B) 19
C) 20
D) 21
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 21 :
Halle el rango de la siguiente función cuadrática:
A) [– 3 ; 0 ]
B) [– 19/2 ; 3 ]
C) [– 3 ; 19/2 ]
D) [ 0 ; 19/2 ]
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 22 :
Resolver la siguiente inecuación:
A) [ –13 ; – 11/2 ]
B) ] – ∞ ; – 13 ]∪[ –11/2 ; +∞ [
C) ] – ∞ ; – 13 [ ∪] –11/2 ; +∞ [
D) ] –13 ; – 11/2 ]
E) Ø
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 23 :
Si el par ordenado (x0 ; y0) es la solución del siguiente sistema.
x + ay = b
bx + 2y = a
Calcular “a+b”
siendo x0=1 ∧ y0=2
A) –10
B) –12
C) –13
D) –14
E) 0
RESOLUCIÓN :
Si x0=1 ∧ y0=2 en el sistema se tiene:
1 + 2a = b
b + 4 = a
Resolviendo se tiene que:
a= – 5 y b=– 9
→ a+b=–14
Rpta. : "D"
PREGUNTA 24 :
Al dividir un polinomio P(x) entre x+a el residuo es b y al dividir P(x) entre x+b el residuo es a, calcular la suma de coeficientes del residuo de dividir P(x) entre (x+a)(x+b)
A) a+b–1
B) a–b–1
C) a+b+2
D) –a–b–1
E) a+b+1
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 25 :
Luego de factorizar el siguiente polinomio
P(x)=x³ – x²–4x+4, se obtiene (x+a)(x+b)(x+c)
Calcular a+b+c
A) –1
B) 1
C) 2
D) –2
E) 0
RESOLUCIÓN :
Factorizando:
P(x)=x³ – x²–4x+4
⇒ P(x)=x²(x–1)–4(x–1)
⇒ P(x)=(x–1)(x² – 4)
⇒ P(x)=(x–1)(x+2)(x–2)
Reconociendo un valor para:
a=–1, b=2, c=–2
→ a+b+c=–1
Rpta. : "A"
PREGUNTA 26 :
Diga usted por qué cuadrante no pasa la siguiente función f: ℜ→ℜ cuya regla de correspondencia viene dado por:
f(x)=–x²+10x–20
A) I y III
B) I y II
C) II
D) III y IV
E) IV
RESOLUCIÓN :
Rpta. : "C"
PREGUNTA 27 :
La ecuación de la recta cuya gráfica se muestra a continuación
es:
A) 2y+3x–6=0
B) 3y–2x+6=0
C) 2y–3x–6=0
D) 3y+2x– 1=0
E) 3y+2x–6=0
RESOLUCIÓN :
Según la gráfica se tiene que
y=ax+b
donde b=2
→ y=ax+2
Luego para x=3, y=0 reemplazando y despejando se tiene:
3y+2x–6=0
Rpta. : "E"
PREGUNTA 28 :
Halla la ecuación de la parábola cuya gráfica se muestra a continuación.
A) y = 2(x–3)² +1
B) y = 2(x–1)² +3
C) y = (x–1)² +3
D) y = (x–2)² +3
E) y = 3(x–1)² +2
RESOLUCIÓN :
Según la gráfica se tiene que:
f(x)=a(x–1)² +3
para x=0 , y=5, se tiene:
a+3=5 → a=2
Luego, la ecuación es
f(x)=y=2(x–1)² +3
Rpta. : "B"
PREGUNTA 29 :
Halla la ecuación del semiplano que pasa por el origen y que se limita con la recta (sin tocarla) que pasa por los puntos (1;3) y (4;2)
A) 3y–x > 10
B) x+3y > 10
C) –3y+x < 10
D) x+2y < 10
E) x+3y < 10
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 30 :
El ingreso de cierta empresa está dado por:
I(x)= – x²+80x+650 , según ello calcula el máximo ingreso.
A) 2250
B) 2350
C) 2025
D) 1850
E) 3200
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 31 :
Siendo:
2<|x|<7 ∧ 1<|y|<5
Calcula el menor valor de la suma “x+y”.
Si: x, y ∈ Z
A) –8
B) 10
C) –5
D) 5
E) –10
RESOLUCIÓN :
De las desigualdades se tiene:
2<|x|<7 ↔ –7<x<–2 ∨ 2<x<7
1<|y|<5 ↔ –5<y<–1 ∨ 1<y<5
El mínimo valor de “x+y” se tiene cuando:
x=-6 ∧ y=-4 → x+y= –10
Rpta. : "E"
PREGUNTA 32 :
Dada la inecuación:
x² – k.x + 9 < 0
Si su conjunto solución es: 〈1;9〉 , indique el valor de "k".
A) 9
B) 12
C) 10
D) 13
RESOLUCIÓN :
Del conjunto solución: 〈1;9〉
1+9= – (– k) ⇒ k=10
Rpta. : "C"
PREGUNTA 33 :
En cierta región marítima, la profundidad y la presión establecen una relación lineal. Se observa lo siguiente: al nivel de la superficie, la presión es de 15 libras/pie², mientras que a 33 pies de profundidad, la presión aumenta a 30 libras/pie². ¿A qué profundidad se deberá descender para que la presión llegue a 40 libras/pie²?
A) 40 pies
B) 45 pies
C) 50 pies
D) 55 pies
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 34 :
El precio de costo de "x" artículos es Pc=5x+2000. Si el precio de venta para cada artículo es 10 soles, halle la cantidad de artículos que se deben producir para no obtener ganancia ni pérdida.
A) 400
B) 1000
C) 600
D) 1200
RESOLUCIÓN :
Para no obtener ganancia ni pérdida:
Pv=Pc
⇒ 10x=5x+2000
⇒ x=400
Rpta. : "A"
PREGUNTA 35 :
Dado un polinomio P(x) de tercer grado con coeficientes enteros, tal que al dividir P(x)÷(x – b) se obtiene el siguiente esquema.
Calcule el valor de abc.
A) – 18
B) – 15
C) – 12
D) – 9
RESOLUCIÓN :
Completando el esquema:
Se plantea:
– 6+b=c ∧ – b+bc=– 12 ∧ – 5+ab=1
• – b+b(b – 6)=– 12
⇒ b² – 7b+12=0
⇒ (b – 4)(b – 3)=0
⇒ b=3 ∨ b=4
• Si b=3
→ c=– 6+3=– 3
→ – 5+a(3)=1 a=2
• Si b=4
→ c=– 6+4=– 2
→ – 5+a(4)=1
⇒ a=3/2
(debe ser entero)
Entonces: a=2; b=3; c=– 3
Finalmente: abc=– 18
Rpta. : "A"
PREGUNTA 36 :
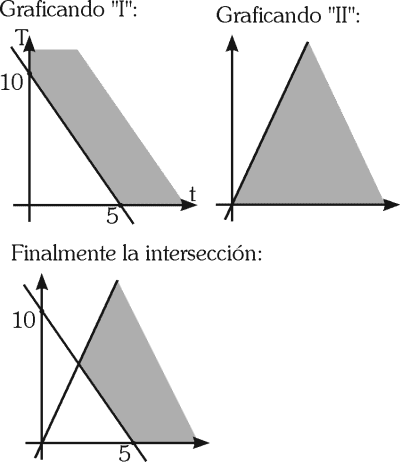
RESOLUCIÓN :
Rpta. : "C"