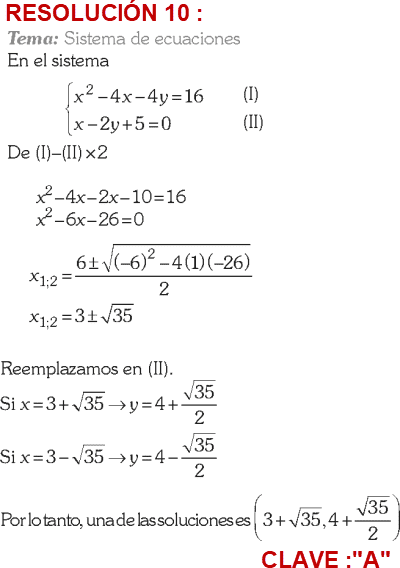ÁLGEBRA PREGUNTAS RESUELTAS ADMISIÓN UNIVERSIDAD SIMULACRO SOLUCIONARIO PRUEBA DE INGRESO DESARROLLADA 2022 2023
PREGUNTA 1 :
Halla el exponente de x en la expresión:
A) 6
B) 7
C) 8
D) 5
E) 4
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 2 :
Si: a² + b² = 1
Determina : M = (a⁴ + b⁴) – (a⁶ + b⁶)
a) a²b²
b) a³ + b³
c) a³b³
d) ab
e) a² – b²
RESOLUCIÓN :
Rpta. : "A"
PREGUNTA 3 :
Sabiendo que :
determina N²+ 1
A) 1/4
B) 2/5
C) 1/5
D) 1/2
E) 5/4
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 4 :
Determina el valor de verdad de las siguientes proposiciones:
I. a²+b²= (a + b)²
II. (a – b)²=a² – 2ab + b²
III. (a + b)³=a³ + b³
A) VFV
B) FVF
C) VFF
D) FVV
E) FFF
RESOLUCIÓN :
PRODUCTOS NOTABLES
Analizamos cada proposición.
I. FALSO
(a + b)²=a² + 2ab + b² ≠ a²+b²
II. VERDADERO
(a – b)² = a² – 2ab + b²
III. FALSO
(a + b)³= a³ + b³ +3ab(a+b) ≠ a³ + b³
Rpta. : "B"
PREGUNTA 7 :
Las raíces de la ecuación cuadrática x²+ax +b= 0 verifican el sistema:
3x₁ + x₂ =3
x₁ + 3x₂ =– 7
Determina el valor de a – b
A) 6
B) 7
C) 4
D) 3
E) 5
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 8 :
Si la ecuación x²+x – 3= 0 tiene por raíces a m y n, determina el valor de m³+n³
A) 10
B) 12
C) –12
D) –10
E) –9
RESOLUCIÓN :
Usando las propiedades de suma y producto de las raíces (Cardano):
m+n= – 1
mn= – 3
Elevamos al cubo. (m+n)³= (–1)³
Se obtiene m³+n³+3mn(m+n) = –1
Reemplazamos :
m³+n³+ 3(–3)(–1) = –1 ⇒ m³+n³+9= –1
⇒ m³+n³= –10
Rpta. : "D"
PREGUNTA 12 :
Dada la siguiente inecuación:
El conjunto solución tiene la forma: determina el valor de: a + b
a) 4
b) 5/2
c) 2
d) 5/3
e) 3/2
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 14 :
Se desea confeccionar una cantidad de pulseras, con una serie de cordones azules y amarillos, con una serie de características. Deben tener al menos más de 20 y menos de 25 cordones. Los cordones amarillos deben ser menos de 10 y más de la mitad de los cordones azules. Determina cuántas pulseras diferentes se pueden confeccionar.
a) 9
b) 5
c) 8
d) 7
e) 6
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 15 :
Al resolver la inecuación: |x⁴ – 48| ≥ |x²|² + 4x² ; Identifica el intervalo solución.
a) [–1; 3]
b) Ø
c) ] –2; 2]
d) [–2; 2]
e) ] –1; 3]
RESOLUCIÓN :
Rpta. : "D"
PREGUNTA 16 :
Determina el valor de a+b+ c, si el término central del desarrollo del cociente notable:
es (x^c) y³⁰
A) 119
B) 128
C) 110
D) 117
E) 125
RESOLUCIÓN :
Rpta. : "E"
PREGUNTA 19 :
Dada la matriz
halla la traza de aquella matriz B que sumada con la matriz A origina la matriz identidad.
A) 4
B) – 4
C) – 2
D) 5
E) 2
RESOLUCIÓN :
Rpta. : "B"
PREGUNTA 20 :
Calcula el determinante de A.
Si A=2C – 3B
Siendo
A) 110
B) 111
C) 109
D) 113
E) 112
RESOLUCIÓN :
PREGUNTA 1 :
Si el polinomio x³ – x² – 4x + 4
se puede representar por (x+a)(x+b)(x+c), tal que a >b >c.
Halle 2a + b – c.
A) – 2
B) 5
C) – 1
D) 3
E) 4
PREGUNTA 2 :
Sean los polinomios
P(x) = ax² + x + 6
Q(x) = ax – 3a
tal que al dividir P(x) entre Q(x) se obtiene como residuo 18.
Calcule P(a + 1).
A) 10
B) 11
C) 12
D) 13
E) 14
PREGUNTA 3 :
Si P(x) = x³ + ax² + 2x + 1 se divide entre (x – 2) el residuo es 21.
Halle P(3).
A) 49
B) 50
C) 51
D) 52
E) 42
PREGUNTA 4 :
Sea la ecuación cuadrática x² – (m – 12)x + 5 = 0 que presenta como conjunto solución el mismo valor numérico con signos opuestos, halle “m”.
A) 12
B) 13
C) 14
D) 15
E) 19
PREGUNTA 5 :
Indique los valores de “b” para que el CS de la siguiente inecuación sea todos los reales.
x² – 2bx ≥ 9 – 10b
A) ]– 1;9]
B) [1;9]
C) ]1;9[
D) ]– 9; – 1[
E) ]2;9[



.png)

.png)
.png)
.png)
.png)

.png)
.png)
.png)
.png)
.png)

.png)
.png)
.png)
.png)
.png)
.png)
.png)



.png)
.png)
.png)
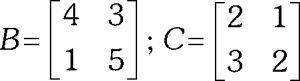


.png)