HABILIDAD LÓGICO MATEMÁTICA SAN MARCOS DECO EXAMEN DE ADMISIÓN UNIVERSIDAD DESARROLLADO PREGUNTAS RESUELTAS DE RAZONAMIENTO MATEMÁTICO

PREGUNTA 16 :

A un listón de madera se le hace 4 cortes simples, de tal forma que las longitudes de los tramos obtenidos están en progresión aritmética de razón 4 cm. Si el listón tuvo 80 cm de largo, ¿cuánto mide uno de los tramos?

A) 28 cm

B) 4 cm

C) 18 cm

D) 20 cm

PREGUNTA 17:

La figura adjunta muestra dos balanza que se encuentran en equilibrio. Si objetos idénticos tienen el mismo peso, y el peso de cada pesa es el que se indica, ¿cuál es el peso de la jarra?

A) 650 g

B) 500 g

C) 700 g

D) 600 g

PREGUNTA 18 :

En una reunión se encuentran tres amigos Paúl, Raúl y Saúl, cuyas edades son tres múltiplos de 8, consecutivos y no necesariamente en algún orden. Además, se tiene la siguiente información:

I. La edad promedio de dos de ellos es igual a la edad del tercero.

II. La edad del mayor de ellos es un cubo perfecto de dos cifras.

III. La diferencia de edades entre el mayor y el menor de ellos es 16 años.

Entonces, para determinar la edad del menor de los amigos es suficiente

A) II

B) I y III

C) Solo I

D) Solo III

PREGUNTA 19 :

Una bolsa completamente oscura contiene 100 boletas, de forma idéntica, numerados del 1 al 100. ¿Cuántos boletos, como mínimo, deben ser extraídos al azar de la bolsa para tener la certeza de haber sacado 3 boletos con numeración impar de 2 cifras?

A) 50

B) 58

C) 53

D) 45

PREGUNTA 20 :

Lea los siguientes enunciados:

– Ningún congresista es luchador.

– Todos los estudiantes son luchadores.

La deducción correcta es

A) todo los estudiantes son congresistas.

B) algunos estudiantes son congresistas.

C) ningún estudiante es congresista.

D) algunos estudiantes no son congresistas.

PREGUNTA 21 :

André, Boris, Carlos, Davis y Evaristo han participado en una carrera de 100 metros planos. Cuando se le preguntó a cada uno por el ganador de la carrera, todos respondieron de la siguiente manera:

– André: «Boris fue el ganador».

– Boris: «Carlos ganó».

– Carlos: «David ganó».

– David: «Yo no gané la carrera».

– Evarito: «Yo no gané la carrera».

Si hubo un único ganador y solo una de las afirmaciones es verdadera, mientras que las demás son falsas, ¿quién ganó la carrera?

A) André

B) Evaristo

C) Boris

D) David

PREGUNTA 22:

Se tiene 6 esferas que, a simple vista, son idénticas excepto por sus pesos. Se sabe que dos de ellas pesan 80 g cada una y que las otras cuatro esferas pesan 78 g cada una. ¿Cuántas pesados, como mínimo, se deben realizar en una balanza de dos platillos para identificar con toda seguridad las esferas más pesadas?

A) 2

B) 4

C) 3

D) 5

PREGUNTA 23 :

En una campaña de recolección de botellas de plástico, los vecinos de una comunidad aportaron 12 botellas en el primer mes y cada uno de los meses siguientes aportaron una botella más que el mes anterior. Si al término de la campaña aportaron un total de 285 botellas, ¿cuántos meses duró la campaña?

A) 15 meses

B) 18 meses

C) 16 meses

D) 17 meses

PREGUNTA 24:

En una maqueta, un arquitecto está replicando la catedral de Lima. Entre las 3 y 4 de la tarde, se da cuenta de que las manecillas del reloj de la catedral forman un ángulo α, tal como se muestra en la figura adjunta. Halle la medida del ángulo α.

A) 174°

B) 162°

C) 156°

D) 168°

PREGUNTA 25 :

María y Ana tienen la siguiente conversación:

María: Cuando nací tú tenías 10 años.

Ana: Dentro de 20 años, mi edad será el triple de la edad actual de Inés.

Si las edades actuales de María, Ana e Inés suman 90 años, ¿qué edad tiene Inés?

A) 20 años

B) 25 años

C) 30 años

D) 15 años

PREGUNTA 26:

Un pequeño robot es programado para recorrer todos los segmentos de una estructura, la cual está representada en la figura adjunta, en una escala de 1 a 20. Es decir, un 1 cm en la figura equivale de 20 cm de longitud real. Además, en la estructura, las líneas horizontales son paralelas al igual que las líneas verticales. ¿Cuál es la menor longitud que puede tener este recorrido? Dé como respuesta la longitud real.

A) 90 m B) 17,40 m C) 16 m D) 18 m

PREGUNTA 27:

Las torres mostradas han sido construidas con piezas cúbicas idénticas a la que muestra la figura 1. Determine el número de cubos que tendrá la torre de la figura 10.

A) 2025

B) 2500

C) 3025

D) 2916

PREGUNTA 28:

Un arquitecto está diseñando el plano de un parque que tiene la forma de un paralelogramo, el cual está representado en la figura adjunta. El arquitecto decide cambiar la posición del parque, para lo cual realiza dos reflexiones. La primera y la segunda reflexión del paralelogramo se realizan tomando como eje de simetría el eje X y el eje Y, respectivamente. Halle las abscisas de los vértices de la figura que se obtiene luego de realizar ambas reflexiones. Dé como respuesta la suma de estas.

A) – 4

B) – 8

C) – 6

D) – 10

PREGUNTA 29:

En un campeonato de fulbito participaron 3 equipos: A, B y C. La tabla adjunta muestra la cantidad de goles a favor (GF) y goles en contra (GC) de los tres equipos, luego de que jugaron todos entre sí, una única vez. Sin embargo, dos casilleros de la tabla no han sido completados. Si el equipo C empató todos sus partidos, ¿cuál fue el resultado del partido A vs. B, en ese orden?

A) 8 - 4

B) 5 - 3

C) 6 - 4

D) 6 - 3

PREGUNTA 30:

En una feria de ciencia hay dos tipos de objetos que llamaron la atención a Carlos: las botellas de Klein y las cintas de Moebius, en donde cada una de ellas tienen etiquetados sus precios, tal como muestra la figura adjunta. Carlos, impactado por las características y propiedades de estos objetos, decide comprar dos botellas de Klein y una cinta de Moebius, pagando por estas un total de S/cba. Halle los dígitos a, b y c. Dé como respuesta a – b+c.

A) 2

B) 4

C) 10

D) – 3

CLAVES DE RM : 16)D 17)D 18)A 19)B 20)C 21)B 22)C 23)A 24)A 25)A 26)D 27)C 28)C 29)D 30)A

SOLUCIONARIO

CLICK AQUÍ Ver SOLUCIONARIO SAN MARCOS ACTUAL

PREGUNTA 1 :

María, Norma, Carla y Elena trabajan en un hospital; todas tienen una sola y distinta profesión: enfermera, obstetra, nutricionista y farmacéutica, no necesariamente en ese orden. Una paciente de este hospital recibió la ayuda incondicional de estas cuatro trabajadoras. Por la ayuda que le brindaron, la paciente le quiere agradecer a cada una de ellas. Sin embargo, no sabe qué profesión tienen. Luego de indagar, solo sabe lo siguiente:

► María y Carla conocen a la obstetra.

► Norma y la nutricionista estuvieron en el consultorio de la farmacéutica.

► la nutricionista es prima de Elena y trabaja en un horario distinto al de María;

► María conoce a la enfermera, pero no a Elena.

Entonces, es cierto que:

A) Norma es farmacéutica.

B) María es nutricionista.

C) Carla es enfermera.

D) Elena es obstetra.

PREGUNTA 2 :

Un cliente llega a una tienda de repuestos para comprar un par de llantas de cierto modelo de alta calidad. El administrador del local sabe que hay tres tipos de calidades de llantas de dicho modelo: 7 ; 5 y 16 llantas de calidades baja, media y alta, respectivamente. Sin embargo, el encargado de las ventas no está y el administrador no sabe diferenciar las calidades, ya que los tres tipos de llantas le parecen idénticas. Como el cliente sí sabe hacerlo, el administrador decide sacar una cierta cantidad de llantas para que el cliente elija. ¿Cuántas llantas, como mínimo, debe mostrar el administrador para tener la certeza de obtener las dos llantas de alta calidad? Dé como respuesta la suma de sus cifras.

A) 9 B) 7 C) 5 D) 4

PREGUNTA 3 :

Mario tiene 22 trozos de papel, algunos de los cuales son de forma cuadrada y el resto de forma triangular. Corta 6 de los trozos cuadrados por una de sus diagonales de vértice a vértice. Luego cuenta el número total de vértices de los 28 trozos de papel obtenidos y observa que hay 90 vértices. ¿Cuántos cuadrados tenía antes de hacer los cortes?

A) 10 B) 11 C) 13 D) 12

PREGUNTA 4 :

Sandra desea visitar a su abuela durante 32 días consecutivos. Su abuela lee sus libros de cuentos los viernes, martes y miércoles. Si Sandra quiere pasar el mayor número de días leyendo cuentos con su abuela, ¿qué día de la semana debería comenzar su visita?

A) Viernes B) Lunes

C) Miércoles D) Martes

PREGUNTA 5 :

Un médico prescribe a Miguel los siguientes medicamentos: 2 pastillas del tipo A cada seis horas y 1 pastilla del tipo B cada ocho horas. Además, le indica que el tratamiento terminará cuando haya tomado 50 pastillas en total. Si Miguel empieza el tratamiento tomando ambos tipos de pastillas, ¿cuántas horas, como mínimo, durará el tratamiento?

A) 104 B) 102 C) 108 D) 96

PREGUNTA 6:

En un campeonato de clasificatorias para la división sub-17 de cierto club de fútbol, quedaron como finalista tres equipos: A, B y C. Estos se enfrentaron en una última ronda triangular, en donde cada equipo jugó solamente una vez con los otros. Los resultados de goles a favor y de goles en contra se anotaron en una tabla; sin embargo, se olvidaron de llenar una casilla, tal como se muestra a continuación:

¿Cuál fue el resultado entre los equipos A y C, en ese orden, si se sabe que los equipos A y B empataron?

A) 3 - 2 B) 4 - 5 C) 5 - 3 D) 3 - 4

PREGUNTA 7 :

Dedicado al negocio de ventas de computadoras, un empresario ha comprado cierta cantidad de laptops de tres tipos: M, N y P, las que cuestan S/840, S/1260 y S/1386, respectivamente. Además, se conoce la siguiente información:

I. El número total de laptops de los tres tipos comprados es 32.

II. La compra total de laptops de los tres tipos es S/40 320.

III. Si solo hubiera comprado 5 laptops del tipo M y 2 del tipo N, el pago total sería S/6720.

IV. La compra incluye, al menos, dos de cada tipo y las del segundo tipo son las de mayor cantidad.

Luego, para determinar el número de laptops comprados de cada tipo, es suficiente la información de los enunciados.

A) I, II y IV.

B) I y II solamente.

C) I, II y III.

D) II y IV solamente.

PREGUNTA 8:

Raúl fabricó una cometa cortando un listón de madera recto en seis piezas. Usó dos de ellas, de longitudes 114 cm y 76 cm, como diagonales tales que formaban dos triángulos rectángulos isósceles idénticos. Las piezas restantes conectaban los puntos medios de los lados de la cometa, como muestra la figura. ¿Cuánto media el listón antes de cortarlo?

A) 360 cm B) 380 cm C) 370 cm D) 390 cm

PREGUNTA 9:

El siguiente gráfico muestra la distribución de los gastos mensuales de una familia. Si el gasto en vivienda y el gasto en alimentos están en la relación como 2 es a 3, y el gasto familiar mensual es S/2400, ¿cuánto más se gasta en alimentos que en vivienda?

A) S/240 B) S/288 C) S/144 D) S/256

PREGUNTA 10:

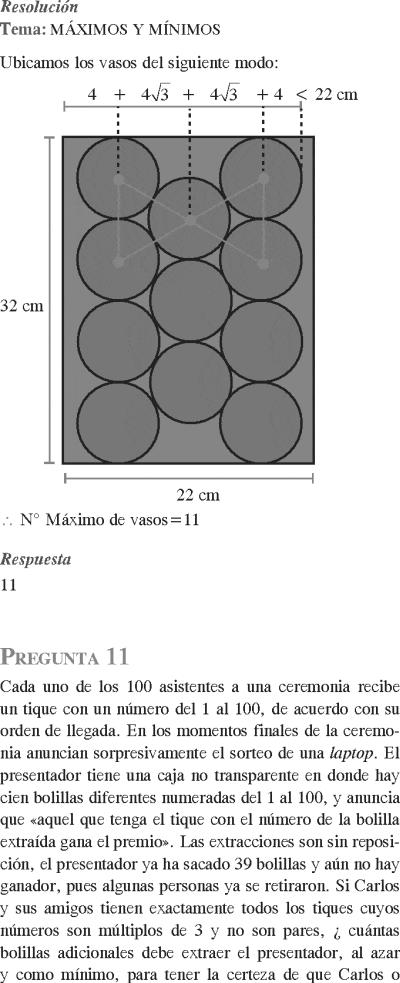
La figura 1 representa un vaso que tiene la forma de un cilindro circular recto cuyo radio de la base mide 4 cm y la figura 2 representa una bandeja rectangular. ¿Cuántos vasos idénticos como los de la figura 1 se pueden colocar, como máximo, sobre la bandeja representada por la figura 2, sin que estos se desborden ni se apilen uno sobre otro?

A) 10 B) 12 C) 14 D) 11

PREGUNTA 11 :

Cada uno de los 100 asistentes a una ceremonia recibe un tique con un número del 1 al 100, de acuerdo con su orden de llegada. En los momentos finales de la ceremonia anuncian sorpresivamente el sorteo de una laptop. El presentador tiene una caja no transparente en donde hay cien bolillas diferentes numeradas del 1 al 100, y anuncia que «aquel que tenga el tique con el número de la bolilla extraída gana el premio». Las extracciones son sin reposición, el presentador ya ha sacado 39 bolillas y aún no hay ganador, pues algunas personas ya se retiraron. Si Carlos y sus amigos tienen exactamente todos los tiques cuyos números son múltiplos de 3 y no son pares, ¿ cuántas bolillas adicionales debe extraer el presentador, al azar y como mínimo, para tener la certeza de que Carlos o alguno de sus amigos gane la laptop? Dé como respuesta la suma de sus cifras.

A) 6 B) 13 C) 9 D) 10

PREGUNTA 12:

Sobre una mesa hay vasos transparentes idénticos en fila: 32 están vacíos y 32 están llenos de vino tinto y en la disposición que muestra la figura. ¿Cuál es el mínimo número de vasos que deben ser movidos para que aparezcan todos los vasos llenos en un lado y todos los vacíos en el otro?

A) 14 B) 18 C) 20 D) 16

PREGUNTA 13 :

Después de salir tarde de una reunión, Inés regresa a casa. Al preguntársele por el lugar donde estuvo, contestó; «He ido a la casa de la madre de la madre del padre de la hermana del hijo de la madre de la hija de mi hermano». Es decir, Inés visitó a su

A) madre. B) hija.

C) abuela. D) tía.

PREGUNTA 14:

El gráfico muestra los resultados obtenidos en una encuesta realizada a un grupo de postulantes con la finalidad de determinar la carrera de su preferencia.

Si, de los encuestados, 135 son mujeres que postulan a la carrera de Matemática, ¿cuántas de las personas encuestadas postulan a la carrera de Física?

A) 480 B) 460 C) 420 D) 360

PREGUNTA 15:

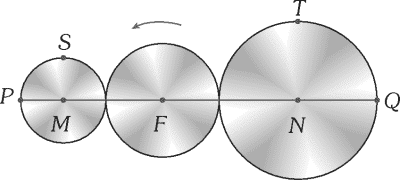
El sistema de tres poleas tangentes de la imagen muestra que los radios de las poleas M y N miden 6 cm y 10 cm, respectivamente. Además, los puntos P, S, T y Q están sobre las circunferencias de las poleas. ¿Cuántas vueltas, como mínimo, debe dar la polea N para que los puntos P y Q se ubiquen simultáneamente en las posiciones iniciales de los puntos S y T, respectivamente, por tercera vez?

A) 6,75 B) 8,75 C) 5,75 D) 7,75

CLAVES DE RM : 1)D 2)C 3)D 4)D 5)A 6)A 7)A 8)B 9)B 10)D 11)C 12)D 13)C 14)D 15)A

SOLUCIONARIO

PREGUNTA 1 :

A) 28 cm

B) 4 cm

C) 18 cm

D) 20 cm

PREGUNTA 2 :

En una reunión se encuentran tres amigos Paúl, Raúl y Saúl, cuyas edades son tres múltiplos de 8, consecutivos y no necesariamente en algún orden. Además, se tiene la siguiente información:

I. La edad promedio de dos de ellos es igual a la edad del tercero.

II. La edad del mayor de ellos es un cubo perfecto de dos cifras.

III. La diferencia de edades entre el mayor y el menor de ellos es 16 años.

Entonces, para determinar la edad del menor de los amigos es suficiente

A) II

B) I y III

C) Solo I

D) Solo III

PREGUNTA 3 :

A) 50

B) 58

C) 53

D) 45

PREGUNTA 4 :

Lea los siguientes enunciados:

– Ningún congresista es luchador.

– Todos los estudiantes son luchadores.

La deducción correcta es

A) todo los estudiantes son congresistas.

B) algunos estudiantes son congresistas.

C) ningún estudiante es congresista.

D) algunos estudiantes no son congresistas.

PREGUNTA 5 :

André, Boris, Carlos, Davis y Evaristo han participado en una carrera de 100 metros planos. Cuando se le preguntó a cada uno por el ganador de la carrera, todos respondieron de la siguiente manera:

– André: «Boris fue el ganador».

– Boris: «Carlos ganó».

– Carlos: «David ganó».

– David: «Yo no gané la carrera».

– Evarito: «Yo no gané la carrera».

Si hubo un único ganador y solo una de las afirmaciones es verdadera, mientras que las demás son falsas, ¿quién ganó la carrera?

A) André

B) Evaristo

C) Boris

D) David

PREGUNTA 6 :

A) 2

B) 4

C) 3

D) 5

PREGUNTA 7 :

A) 15 meses

B) 18 meses

C) 16 meses

D) 17 meses

PREGUNTA 8 :

María y Ana tienen la siguiente conversación:

María: Cuando nací tú tenías 10 años.

Ana: Dentro de 20 años, mi edad será el triple de la edad actual de Inés.

Si las edades actuales de María, Ana e Inés suman 90 años, ¿qué edad tiene Inés?

A) 20 años

B) 25 años

C) 30 años

D) 15 años

HABILIDAD LÓGICO MATEMÁTICA SAN MARCOS DECO EXAMEN DE ADMISIÓN UNIVERSIDAD DESARROLLADO PREGUNTAS RESUELTAS DE RAZONAMIENTO MATEMÁTICO

Pre U