SOLUCIONARIO SEGUNDO EXAMEN CEPRE SAN MARCOS 2021 II CICLO ORDINARIO INGRESO DIRECTO A LA UNIVERSIDAD DECO CEPUSM PDF
PREGUNTA 1 :
En cada una de las caras de un cubo se ha escrito un número de modo que la suma de los números escritos en caras opuestas siempre es la misma, y no hay dos caras con el mismo número. Si cinco de los números escritos son 14, 11, 9, 6 y 5, halle la suma de las cifras del número escrito en la sexta cara del cubo.
A) 6
B) 8
C) 5
D) 7
PREGUNTA 2 :
En una urna hay 60 fichas numeradas con números enteros desde 1 hasta 60, con un número en cada ficha. Si solo las fichas que han sido numeradas con un múltiplo de 4 están pintadas de color rojo, ¿cuántas fichas, como mínimo, se deben extraer al azar para tener la certeza de haber extraído 2 fichas numeradas con un múltiplo de 3 y que no sean de color rojo?
A) 47
B) 45
C) 46
D) 44
PREGUNTA 3 :
El reloj de Carlos se adelanta 10 minutos cada hora. Cierto día, al salir a trabajar, Carlos colocó la hora correcta en su reloj, siendo esta las 9 a. m. En la noche de ese mismo día, al regresar a su casa, observó que su reloj marcaba las 11 p. m. En ese instante, ¿cuál era la hora exacta?
A) 09:00 p. m.
B) 10:00 p. m.
C) 09:30 p. m.
D) 10:30 p. m.
PREGUNTA 4 :
Gerardo observa que el menor número positivo cuya última cifra es 5 y que tiene 17 divisores propios positivos coincide con la cantidad total de estudiantes que hay en su colegio. Si se sabe que, en dicho colegio, el número de varones supera en 225 al de mujeres, ¿cuántas mujeres hay?
A) 675
B) 3150
C) 1450
D) 375
16.
En la operación mostrada, ¿cuántas fichas numeradas deberán cambiar de posición, como mínimo, para que M asuma el menor valor no negativo posible?
17.
En la cuadrícula que se muestra, escriba un número entero positivo en cada casilla, de tal manera que los cinco números escritos sean todos diferentes y que, además, de izquierda a derecha se cumpla lo siguiente: – La suma de los tres primeros números sea 19. – El producto de los tres últimos números sea 15. – La suma del primer y el penúltimo número sea 11. – Los números estén ordenados de mayor a menor. ¿Cuál es la suma de los números escritos en las casillas extremas de la cuadrícula?
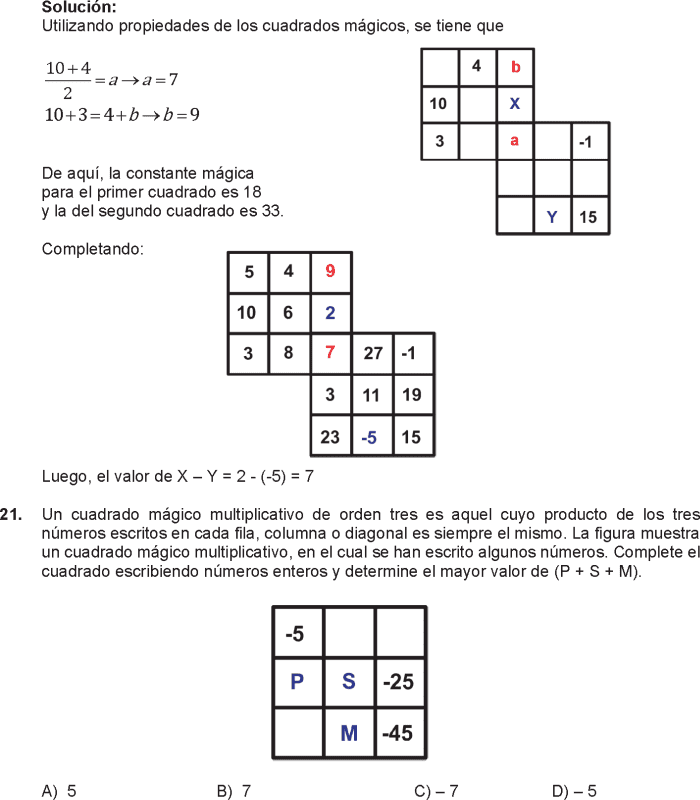
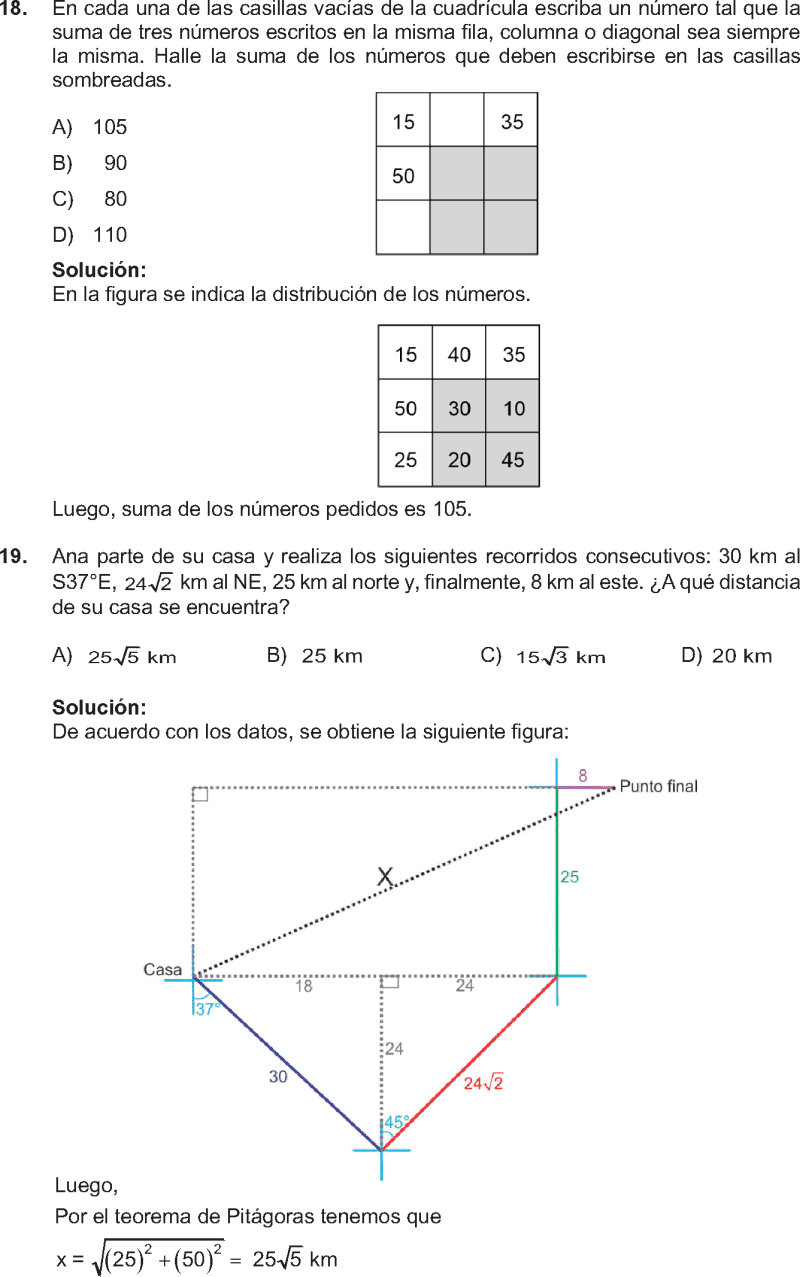
18.
En cada una de las casillas vacías de la cuadrícula escriba un número tal que la suma de tres números escritos en la misma fila, columna o diagonal sea siempre la misma. Halle la suma de los números que deben escribirse en las casillas sombreadas.
19.
Ana parte de su casa y realiza los siguientes recorridos consecutivos: 30 km al S37°E, 24 2 km al NE, 25 km al norte y, finalmente, 8 km al este. ¿A qué distancia de su casa se encuentra?
20.
Carlos tiene una jarra llena con 9 litros de leche y dos jarras vacías (una de 6 litros y la otra de 2 litros de capacidad), como muestra la figura. Ninguna de las tres jarras tiene marcas que permitan hacer mediciones, ni se permite hacer marcas en ellas. Utilizando solamente estas tres jarras y sin desperdiciar leche en ningún momento, ¿cuántos trasvases, como mínimo, debe realizar Carlos para poder obtener 5 litros de leche en uno de estos recipientes?
21.
Si se escriben solamente los números 1, 2 o 3 en las casillas vacías de la cuadrícula, de tal forma que la suma de los cuatro números escritos en una misma fila o columna sea igual a 10, ¿cuál es la suma de los números escritos en las casillas sombreadas?
22.
Sobre una mesa, Yaritza ha colocado cinco discos, como muestra la figura 1. En cada disco, una cara es de color azul y la otra de color rojo. Con el fin de colocar todos los discos con la cara de color rojo hacia arriba, como muestra la figura 2, Yaritza debe realizar cierto número de movimientos. Si en cada movimiento solo se puede voltear un par de discos contiguos a la vez, ¿cuál es el mínimo número de movimientos que debe realizar para lograr el objetivo?
23.
En la secuencia de figuras mostrada, cada figura está formada por palitos idénticos. ¿En cuál de estas figuras se emplean exactamente 101 palitos?
25.
Sobre un tablero no transparente, Rosa colocó cinco dados convencionales, como se muestra en la figura. ¿Cuántos puntos, como mínimo, son visibles para Rosa?
26.
Los cuatro rectángulos de las líneas punteadas de la figura indican el lugar donde deben colocarse cuatro fichas que son parte de un juego completo de dominó para formar un cuadrado. Si Ricardo completó dicho cuadrado, de tal manera que la suma de los puntos en cada lado del cuadrado es la misma y la máxima posible, ¿cuál es el valor de dicha suma?
27.
¿De cuántas maneras diferentes se puede leer la palabra PERA considerando igual distancia mínima de una letra a otra en cada lectura?