SOLUCIONARIO TECER EXAMEN CEPRE SAN MARCOS 2021 2022 CICLO ORDINARIO INGRESO DIRECTO A LA UNIVERSIDAD DECO CEPUSM PDF
PROBLEMA 1 :
Se le pregunta por su edad a Leslye y ella responde: «Si al año en que cumplí 15 años se le agrega el año en que cumplí 20 años, y a esta suma se le resta el año en que nací y el año actual, se obtendría 11 como resultado». Si en el año actual Leslye ya cumplió años, ¿cuántos años tiene Leslye?
A) 24
B) 26
C) 22
D) 20
PROBLEMA 2 :
En su negocio de abarrotes, Betty dispone de un saco con 39 kg de arroz, una balanza de dos platillos y pesas de 2 kg, 3 kg y 9 kg, una de cada tipo. Si un cliente le pide que le despache 17 kg de arroz, ¿cuántas pesadas, como mínimo, debe realizar Betty para atender el pedido del cliente, si en cada pesada debe emplear por lo menos dos pesas?
A) 1
B) 2
C) 3
D) 4
PROBLEMA 3 :
Se tienen seis cajas que contienen canicas y ninguna de ellas está vacía. Si cada caja contiene un número par de canicas distinto del número de canicas de las otras cinco cajas, ¿cuál es el número mínimo de canicas que hay en total en las seis cajas?
A) 12
B) 10
C) 8
D) 14
PROBLEMA 4 :
Eva debe tomar dos pastillas del tipo A cada 3 horas y una pastilla del tipo B cada 7 horas. Si, al inicio, tomó ambas pastillas simultáneamente y tomó 37 pastillas en total, ¿cuánto tiempo, como mínimo, duró su tratamiento?
A) 42 h
B) 39 h
C) 40 h
D) 41 h
PROBLEMA 5 :
En una planta de ensamblaje, hay dos robots que trabajan con absoluta precisión. Ellos colocan puntos de soldadura colineales e igualmente espaciados. El ingeniero de la planta ha observado que el primer robot coloca, en 90 segundos, tantos puntos de soldadura como el tiempo, en segundos, que tarda en colocar dos puntos consecutivos; mientras que el segundo robot coloca cinco puntos de soldadura en 24 segundos, siendo constante también el tiempo que demora en colocar dos puntos consecutivos. Si ambos robots colocan su primer punto de soldadura simultáneamente, ¿cuántos puntos habrá colocado el robot más rápido cuando ambos coincidan por cuarta vez en colocar un punto de soldadura?
A) 16
B) 14
C) 15
D) 13
- CLICK AQUI Ver EXAMEN COMPLETO PDF
- Ver LOS DEMAS EXAMENES RESUELTOS
- Ver SOLUCIONARIO EXAMEN SAN MARCOS ADMISIÓN
- Ver SOLUCIONARIO SIMULACRO SAN MARCOS
- Ver VIDEOS
17.
En la figura se muestra un cubo de madera. ¿Cuántos cortes rectos, como mínimo, debe hacerse a dicho cubo para que quede dividido totalmente en 18 paralelepípedos congruentes?
19.
En las figuras mostradas, la figura 1 representa un tablero de triplay que ha sido cuadriculado y está formado por 35 cuadrados cuyos lados miden 2 cm, y la figura 2 representa una ficha que está formada por 6 cuadrados cuyos lados miden 2 cm. ¿Cuántos trozos congruentes con la figura 2, como máximo, se pueden recortar de la figura 1?
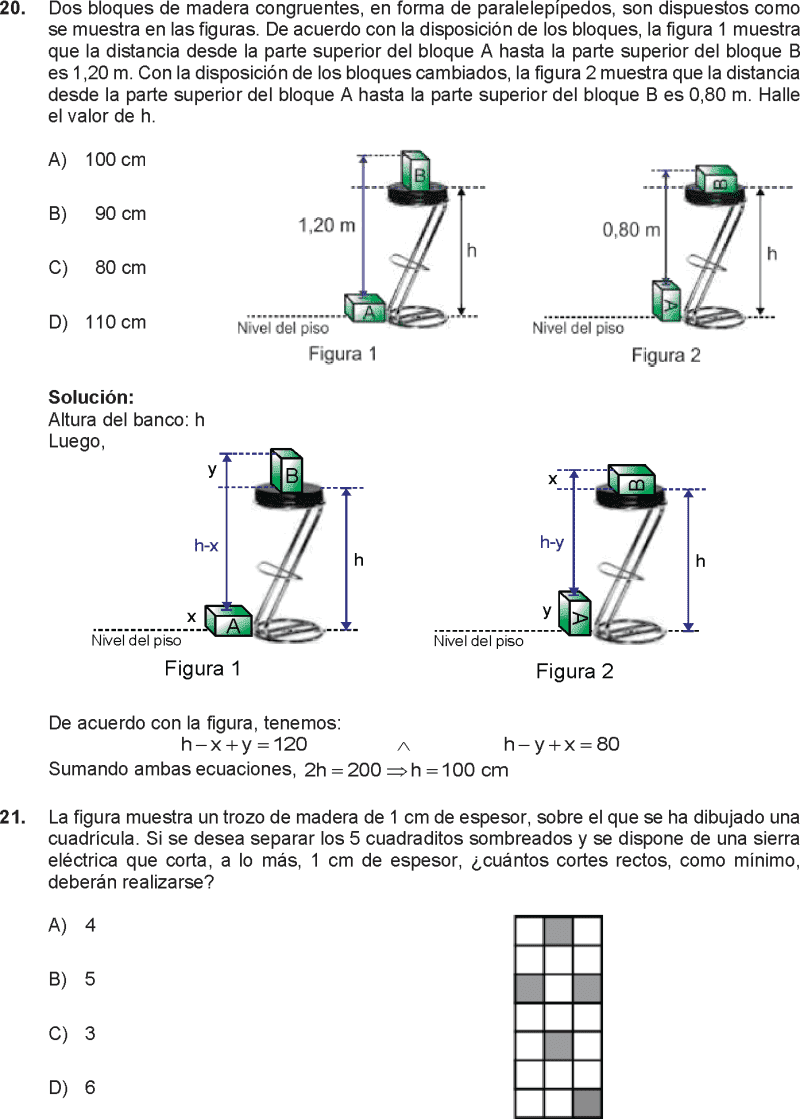
20.
Dos bloques de madera congruentes, en forma de paralelepípedos, son dispuestos como se muestra en las figuras. De acuerdo con la disposición de los bloques, la figura 1 muestra que la distancia desde la parte superior del bloque A hasta la parte superior del bloque B es 1,20 m. Con la disposición de los bloques cambiados, la figura 2 muestra que la distancia desde la parte superior del bloque A hasta la parte superior del bloque B es 0,80 m. Halle el valor de h.
21.
La figura muestra un trozo de madera de 1 cm de espesor, sobre el que se ha dibujado una cuadrícula. Si se desea separar los 5 cuadraditos sombreados y se dispone de una sierra eléctrica que corta, a lo más, 1 cm de espesor, ¿cuántos cortes rectos, como mínimo, deberán realizarse?
23.
Se tiene una lámina con la forma de un hexágono regular cuyos lados miden 3 cm. Dicho hexágono se coloca al borde de una lámina rectangular de 9 cm × 6 cm, tal como muestra la figura. Si la lámina hexagonal gira apoyándose siempre en un vértice y avanza en el sentido indicado alrededor de la lámina rectangular, sin deslizarse, ¿cuál es la mínima longitud que recorre el punto central A hasta el instante en que el hexágono regrese a su posición inicial?
24.
Clara quiere pintar el siguiente cuadro, de modo que dos regiones simples con un lado o parte de un lado en común no tengan el mismo color. ¿Cuántos colores diferentes, como mínimo, debe usar?
27.
En una hoja cuadriculada, Carlos ha dibujado dos rectas perpendiculares. Con dichas rectas trazadas, usa la hoja como un plano coordenado, donde las rectas representan los ejes coordenados y la intersección de estas, el origen de coordenadas. Carlos dibuja un triángulo de vértices A(-6,4), B(1,7) y C(2,-2), como muestra la figura. Luego, dibuja un segundo triángulo simétrico al anterior, usando como punto de simetría el origen de coordenadas. Halle la suma de las coordenadas de los vértices del segundo triángulo.
29.
¿Qué hora muestra el reloj de la figura? 30. En el siguiente sistema, las poleas A y B son tangentes; las poleas B y C tienen un eje común y los radios de las poleas A, B y C miden 40, 30 y 18 cm, respectivamente. Si la esfera M, que es idéntica a N, sube 20 cm, ¿cuántos centímetros sube la esfera N?