GRADOS Y POLINOMIOS PROBLEMAS RESUELTOS PREUNIVERSITARIOS

Los polinomios, están relacionadas con las funciones polinomiales y tienen mucha aplicación en diferentes áreas, por ejemplo en ingeniería el polinomio cuadrático es utilizado para el diseño de estructuras metálicas y de concreto armado.

Al concluir este capítulo estarás en capacidad de : 

☛ Identificar y reconocer polinomios de una o más variables, efectuando operaciones con ellas. 

☛ Determinar el valor numérico de una expresión y realiza cambio de variable. 

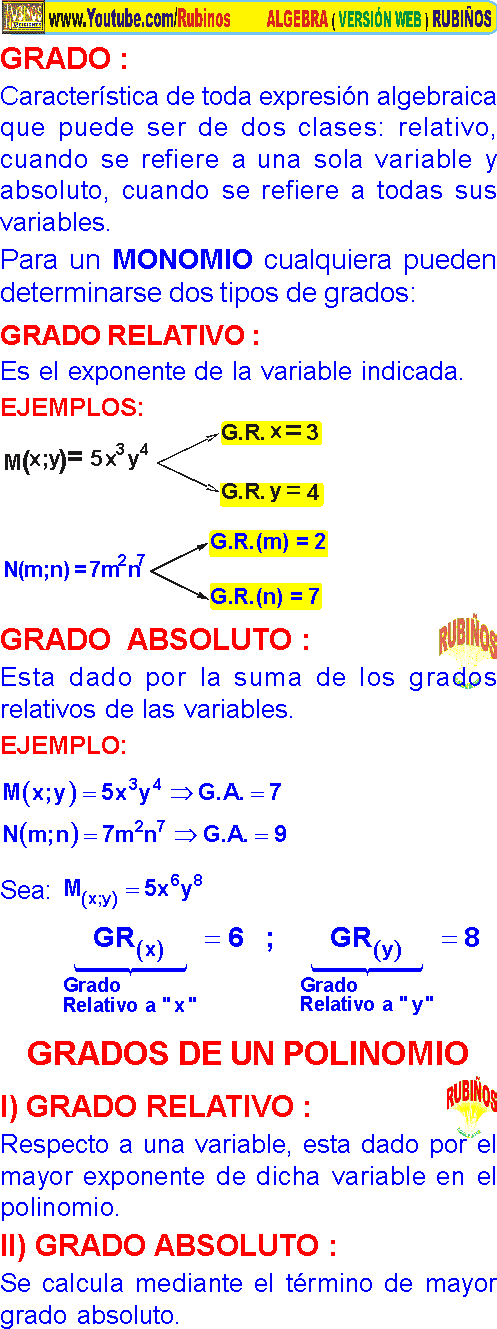
☛ Obtener y calcular el grado relativo y absoluto de polinomios. 

☛ Relacionar y aplicar propiedades de grados de polinomios en la resolución de problemas.

Encontrar las raíces de una ecuación polinómica es uno de los problemas más antiguos en matemáticas. Sin embargo, los conceptos formales y la notación que actualmente utilizarnos para resolver este tipo de problemas solo fueron desarrollados a partir del siglo XV d.n.e. 

Antes de esto, las ecuaciones eran escritas en palabras y no con los símbolos actuales. El matemático francés Francois Viete (1540 - 1603) es considerado uno de los precursores del álgebra moderna. 

En su obra principal, Isagoge Artem Analycitem (Introducción al arte analítico), se presenta por' primera vez una concepción consistente y sistemática de la noción moderna de ecuación algebraica. Viete introduce el uso de símbolos para representar los términos que constituyen una ecuación: vocales para las incógnitas y consonantes para los valores conocidos (coeficientes).