CRONOMETRÍA Y RELOJES FÓRMULAS Y EJEMPLOS
Un reloj es un dispositivo empleado para medir o indicar el paso del tiempo y divide el día en horas, minutos y segundos. Puede ser fijo o portátil.
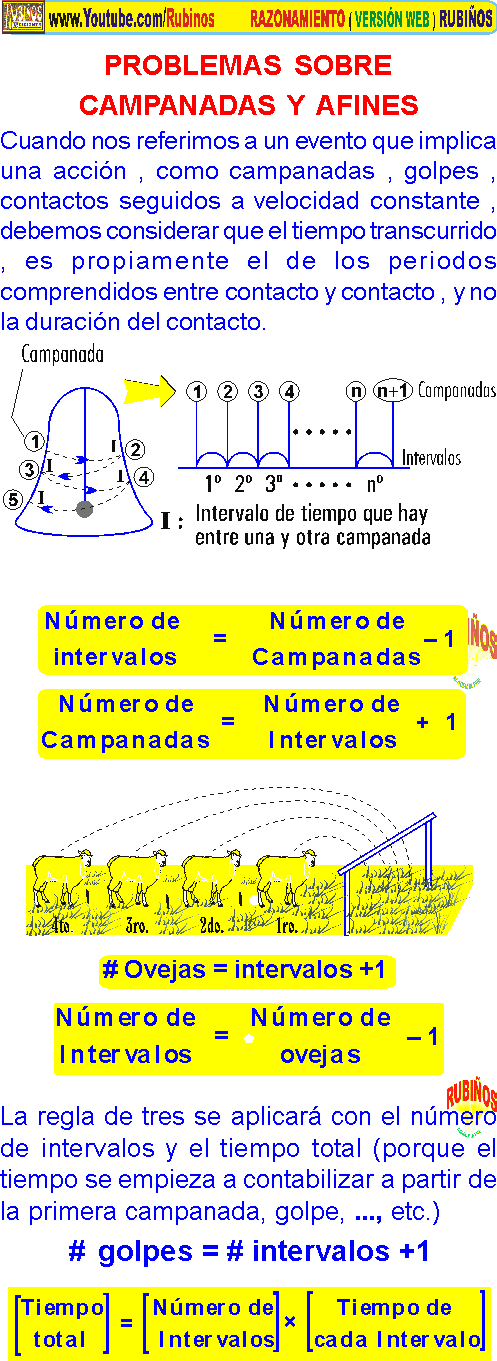
- CLIC AQUÍ Ver CAMPANADAS EJERCICIOS RESUELTOS
- Ver ADELANTOS Y ATRASOS
- Ver TIEMPO TRANSCURRIDO
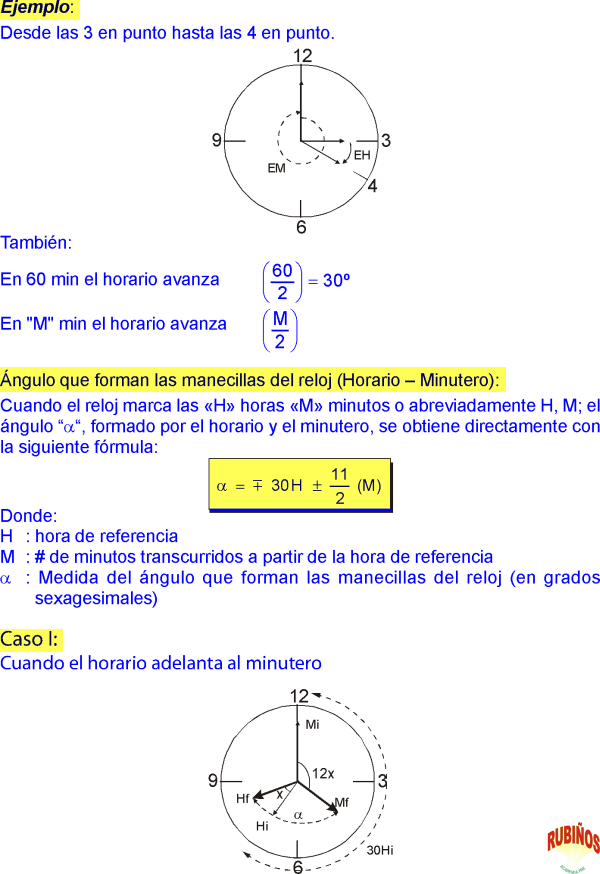
- Ver ÁNGULO CON MANECILLAS
- Ver CRONOMETRÍA FÓRMULAS Y EJEMPLOS
- Ver CRONOMETRÍA PROBLEMAS RESUELTOS
- Ver PRACTICA DE CRONOMETRÍA CON RESPUESTAS
PREGUNTA 1 :
Si las horas transcurridas del día exceden en 4 a los 2/3 de las horas no transcurridas, entonces la hora es :
A) 12:00
B) 13:00
C) 12:45
D) 08:40
E) 08:30
Rpta. : "A"
PREGUNTA 2 :
Si faltan para las 9:00 la mitad de los minutos que pasaron desde las 7:00.
¿Qué hora es?
A) 7:50
B) 8:10
C) 8:20
D) 8:40
E) 8:30
Rpta. : "C"
PREGUNTA 3 :
¿Qué fracción decimal de la hora viene a ser 24 minutos con 36 segundos?
a) 0,52
b) 0,37
c) 0,71
d) 0,41
e) 0,49
Rpta. : "D"
PREGUNTA 4 :
¿Qué día del año marcará la hoja de un almanaque cuando el número de hojas arrancadas excede en dos a los 3/8 del número de hojas que quedan?
a) 11 de abril
b) 12 de abril
c) 13 de abril
d) 10 de abril
e) N.A.
Rpta. : "B"
PREGUNTA 5 :
Si faltan transcurrir del día tanto como ya pasó hasta hace 6 horas.
¿Qué hora es?
a) 6 pm
b) 5 am
c) 3 am
d) 4 pm
e) 3 pm
Rpta. : "E"


































































.gif)
.gif)
.gif)
.gif)














