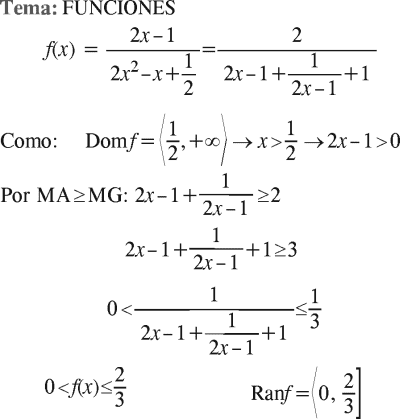ADMISIÓN UNI 2019 I SEGUNDA PRUEBA RESUELTA DE LA UNIVERSIDAD NACIONAL DE INGENIERÍA-MATEMÁTICAS SOLUCIONARIO 2019-1 pdf

PREGUNTA 1 :

El perímetro de un triángulo es 50 m y sobre cada lado del triángulo se forma un cuadrado cuyo lado coincida con el lado del triángulo. Como resultado, la suma de las áreas de los cuadrados formados es 900 m² y el lado del primer cuadrado es al del segundo como, el lado del tercero es a la mitad del primero. La relación del mayor y el menor de los lodos del triángulo es de (Considere que los lados del triángulo son números naturales)

A) 2 a 1

B) 5 a 2

C) 3 a 1

D) 5 a 1

E) 11 a 2

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 2 :

Las magnitudes X e Y son tales que (Y – 2) y (X²+ 1) son inversamente proporcionales. Se sabe que cuando X= 2, se tiene que Y= 3. Determine la ecuación que relaciona X e Y

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 3 :

Cualquier tipo de café crudo pierde el 20% de su peso al tostarlo. Se ha comprado dos tipos de café crudo cuyos precios por kilogramo son 10 y 15 soles respectivamente.

Si todo el café tostado se vendiera a 15 soles el kilogramo no se ganaría ni se perdería, pero se vendió todo el café tostado en S/3240 ganando el 20% del costo. Halle la suma de los pesos iniciales y dé como respuesta la diferencia de la mayor cifra con la menor cifra del resultado.

A) 6

B) 5

C) 4

D) 3

E) 2

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 4 :

El número de hijos por familia en una determinada ciudad es una variable aleatoria H, cuya función de probabilidad es

f(x)=P[H=x]=Kx/5

x = 1; 2; 3; 4; 5

¿Cuál es la probabilidad de que una familia tenga 3 hijos dado que tiene al menos dos hijos?

A) 0,200

B) 0,333

C) 0,214

D) 0,267

E) 0,357

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 5 :

Se tienen 496 números naturales consecutivos. Al dividir el número anterior al mayor entre el número menor de la lista de números, se obtiene como residuo 49 y como cociente un número natural diferente a 6. Indique la cifra de las centenas del número que se obtiene al multiplicar el trigésimo segundo número y el centésimo tercer número.

A) 0

B) 1

C) 2

D) 3

E) 4

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 6 :

Halle un número de la forma

tal que sea múltiplo de44

Dar como respuesta el residuo que se obtiene al dividir dicho número entre 5.

A) 0

B) 1

C) 2

D) 3

E) 4

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 7 :

Calcule:

Dar como respuesta la primera cifra decimal.

A) 0

B) 1

C) 2

D) 3

E) 4

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 8 :

Indique la secuencia correcta después de determinar si la proposición es verdadera (V) o Falsa (F).

I. El producto de un número irracional por otro irracional es siempre irracional.

II. La suma de dos números irracionales siempre es un número irracional.

III. Entre dos números racionales diferentes siempre existe otro número racional.

A) VVV

B) VFV

C) VFF

D) FFF

E) FFV

RESOLUCIÓN :

Tema: Conjunto de los racionales

I. Falso

Veamos un contraejemplo (√3 −1) (√3 +1)=3 −1

irracional×irracional racional

Por lo tanto, el producto de dos números irracionales puede resultar un número racional.

II. Falso

Veamos un contraejemplo (1−√2)+(1−√2)= 2

irracional+irracional racional

Por lo tanto, la suma de dos números irracionales puede resultar un número racional.

III. Verdadero

Se sabe que el conjunto de los números racionales es un conjunto denso; es decir, entre dos racionales cualesquiera hay infinitos racionales.

Por lo tanto, entre dos racionales diferentes siempre existe otro números racionales.

Rpta. : "E"

PREGUNTA 9 :

Sean A, B y D subconjuntos de los números reales y definimos el operador * mediante

A * B= (A ∩ B)^C

Indique el valor de verdad de las siguientes proposiciones.

I. (A * B) * D=A *(B * D)

II. (A * B) * A = A * (B * A)

III. A * ∅ = ∅

Donde A^C indica el complemento de A.

A) VFF

B) FVV

C) VVV

D) FFF

E) FVF

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 10 :

Definimos el conjunto

Considere las siguientes proposiciones:

I. La suma de los elementos del conjunto A es 7.

II. Card(A)=2

III. 2√2−2 ∈A

Determine de las proposiciones dadas cuáles son verdaderas.

A) solo I

B) solo II

C) solo III

D) I y II

E) I y III

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 11 :

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 12 :

Halle el polinomio p(x) de coeficientes racionales de menor grado con raíces 1 y 1+√2, y que además cumpla p(0) = 1.

Dé como respuesta la suma de los coeficientes del polinomio.

A) –2

B) –1

C) 0

D) 1

E) 3

RESOLUCIÓN :

Tema: Polinomios

Del dato se tiene que 1 es una raíz.

Entonces

P(1) =0

Por propiedad

P(1) = suma de coeficientes

→ P(1) =0= suma de coeficientes

Rpta. : "C"

PREGUNTA 13 :

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 14 :

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 15 :

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 16 :

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 17 :

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 18 :

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 19 :

Dado el conjunto S={x∈R / 0 < Log|x –1| < 1}

Determine S ∩ ([0; 2] ∪ [12; 20]).

A)∅

B) 〈1; 2〉

C) [15; 20]

D) [12; 15]

E) [12; 20]

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 20 :

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 21 :

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 22 :

En un triángulo ABC, m∠BAC=2(m∠ACB) = 30°, si se traza la mediana BM, calcule m∠ABM.

A) 75°

B) 80°

C) 90°

D) 100°

E) 105°

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 23 :

El cateto AB del triángulo rectángulo ABC se divide en 8 partes congruentes. Por los puntos de división se trazan 7 segmentos paralelos al cateto AC tal como se muestra en la figura. Si AC= 10 m, halle la suma (en m) de las longitudes de los 7 segmentos.

A) 33

B) 34

C) 35

D) 36

E) 37

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 24 :

En un cuadrilátero ABCD, las diagonales miden AC= 17 cm y BD= 15 cm; sea M punto medio de AC y F punto medio de BD; los ángulos interiores de B y D miden 90°. Calcule MF en cm.

A) 2

B) 3

C) 4

D) 5

E) 6

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 25 :

Al cortarse dos cuerdas de una misma circunferencia perpendicularmente, una de ellas queda dividida en segmentos de 3 y 4 unidades y la otra en segmentos de 6 y 2 unidades. Determine el diámetro de la circunferencia.

A)√87

B)√73

C)√68

D)√65

E)√63

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 26 :

La figura muestra tres semicircunferencias y la longitud de la circunferencia mayor es 10π u. Si AB=√24 u, siendo AB tangente a las semicircunferencias interiores, calcule la longitud (en u) de la circunferencia menor.

A) 2π

B) 3π

C) 4π

D) 5π

E) 6π

RESOLUCIÓN :

Rpta. : "C"

PREGUNTA 27 :

Para tres circunferencias tangentes (exteriormente) dos a dos, la suma de sus radios es 10 cm y el producto de los mismos es 40 cm³. Halle el área (en cm²) de la región triangular cuyos vértices son los centros de la circunferencia.

A) 18

B) 18,5

C) 19

D) 19,5

E) 20

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 28 :

El punto A está a 8 m encima de un plano horizontal P, y el punto B se halla a 4 m encima del mismo plano. Si C es un punto del plano P tal que AC+BC es mínimo y el ángulo que forman la recta ↔CB con el plano P es 53°, entonces (en m) AC es

A) 8

B) 8,5

C) 9

D) 9,5

E) 10

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 29 :

Las caras de un triedro equilátero de vértice V miden 60°. En una de sus aristas se considera un punto R de tal manera que VR= 2 cm. Por R pasa un plano perpendicular a VR que interseca a las otras aristas en S y T. Halle el área del triángulo RST (en cm²).

A) 3√2

B) 2√6

C)√26

D) 3√3

E) 4√2

RESOLUCIÓN :

Rpta. : "E"

PREGUNTA 30 :

Sea el tetraedro regular de arista a, con a un entero positivo diferente de múltiplo de 3. Se unen los baricentros de las caras del tetraedro regular formando un tetraedro nuevo y así se repite el proceso n veces

A) 8√3

B) 16

C) 8√6

D) 16√2

E) 32

RESOLUCIÓN :

Rpta. : "B"

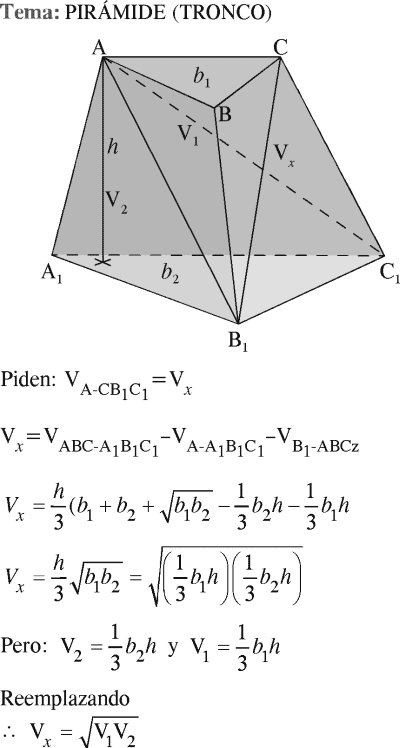
PREGUNTA 31 :

En un tronco de pirámide ABC-A₁B₁C₁, los volúmenes de las pirámides B₁-ABC y A-A₁B₁C₁, miden V₁ y V₂ respectivamente. Determine el volumen de la pirámide A-CB₁C₁.

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 32 :

El volumen de un cono de revolución es 36π cm³. Se inscribe un triángulo equilátero ABC en la base del cono. El triángulo ABC está circunscrito a una circunferencia cuyo círculo es base de un cilindro recto inscrito en el cono. Calcule el volumen del cilindro (en cm³).

A) 27π/10

B) 27π/8

C) 27π/5

D) 27π/2

E) 27π

RESOLUCIÓN :

Rpta. : "D"

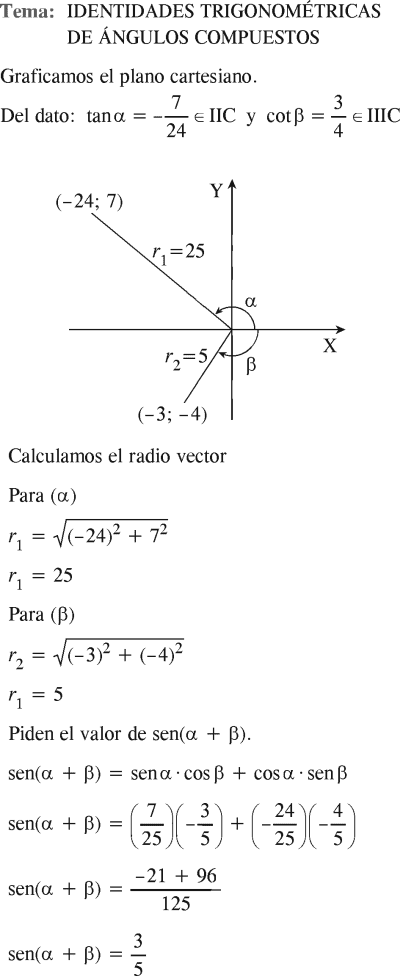
PREGUNTA 33 :

Sea α un ángulo en el II cuadrante con tan(α)=−7/24 y β un ángulo en el III cuadrante con cot(β)=3/4 Determine el valor de sen(α+β).

A) − 107/125

B) − 3/5

C) 17/125

D) 3/5

E) 107/125

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 34 :

Si la gráfica de y=Aarccos(Bx+C) +D es

determine el valor de E=A+B+C.

A) 3

B) 2/3

C) 4/3

D) 4

E) 14/3

RESOLUCIÓN :

Rpta. : "D"

PREGUNTA 35 :

A) 2cos(θ) – sen(θ)

B) cos(θ) – sen(θ)

C) 2sen(θ) – cos(θ)

D) sen(θ) + cos(θ)

E) sen(θ) – cos(θ)

RESOLUCIÓN :

Rpta. : "B"

PREGUNTA 36 :

Obtenga el conjunto solución del siguiente sistema de ecuaciones:

y = 1 – cosx

1 = 4ycosx

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 37 :

Determine el menor periodo positivo de la función definida por

A) π/2

B) π

C) 3π/2

D) 2π

E) 4π

RESOLUCIÓN :

Rpta. : "A"

PREGUNTA 38 :

Un marino que observa el horizonte desde un faro de altura h, lo hace con un ángulo de depresión θ. Calcule el radio R de la Tierra en función de h y θ.